Many hyperlinks are disabled.
Use anonymous login
to enable hyperlinks.
Overview
| Artifact ID: | 70e086ae58fd9782011ac9db88e64669824660e4 |
|---|---|
| Page Name: | Affine Transform |
| Date: | 2015-05-02 21:23:00 |
| Original User: | sandro |
| Parent: | d58fb3a802e01efc38cef7d978be63a4b3361a63 (diff) |
| Next | d811cbd7e2e0c54842fdefebdb7fe9853c8b6f74 |
Content
Affine Transformations
Starting since version 4.3.0 SpatiaLite supports several new SQL functions based on affine transformations; understanding all the underlaying mathematics could easily be a rather difficult task, more notably if you have absolutely no familiarity with this kind of operations.So we'll start smoothly by introducing first a very simple practical example based on kind of a joke about the geography of Italy and Sicily.
Fancy Geograpy and amusing Math
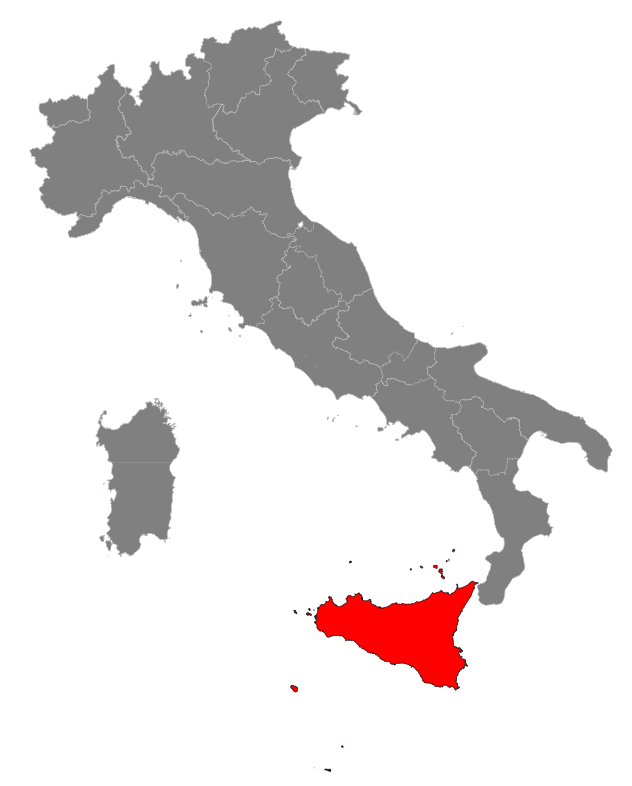
PrefaceLooking to a map of Italy it appears obvious at first glance that Sicily is located in a very inconvenient position:
Incidentally we'll use the new SQL functions based on Affine Transformations for this task. Let's go on. |
|
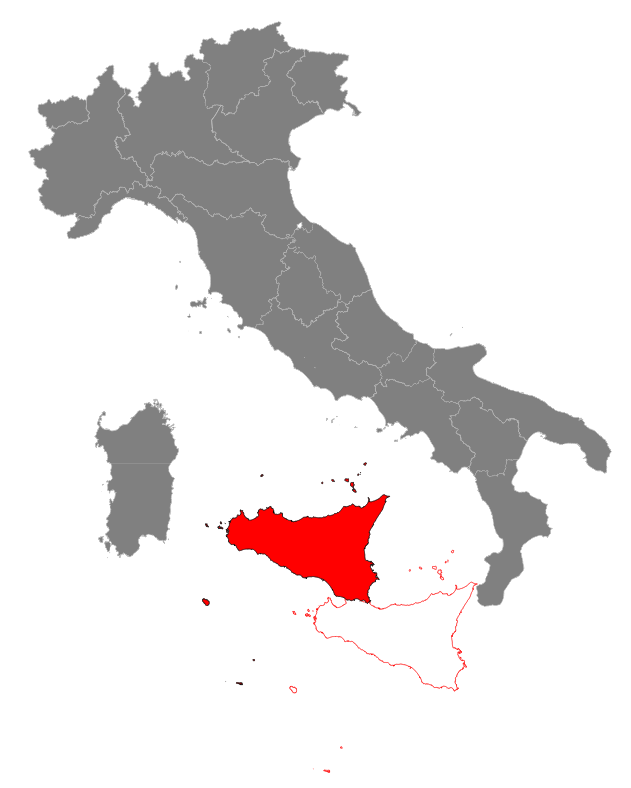
Step #1: translating Sicily into a more convenient positionThere is plenty of free room in the lower Tyrrhenian Sea, so we'll start by applying a translation: this practically means adding (or subctracting) a constant value to the coordinates on both x and y axes.After a very quick examination moving Sicily 150 km (i.e. 150,000 m) westwards and 150 km northwards seems to be an absolutely reasonable choice. So using the Affine Transformation SQL functions we'll write the following SQL statement:
CREATE TABLE sicilia_1 AS
SELECT cod_reg,
ATM_Transform(geometry,
ATM_CreateTranslate(-150000, 150000)) AS geom
FROM sicilia_0;
SELECT RecoverGeometryColumn('sicilia_1', 'geom', 32632, 'MULTIPOLYGON', 'XY');
Remarks:
|
|
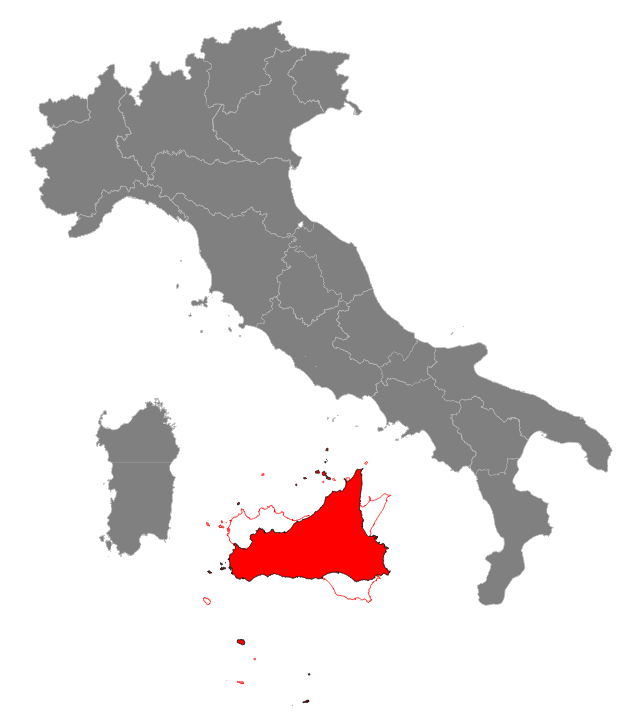
Step #2: rotating Sicily so to get a nice horizontal alignementAligning the southern shores of Sicily to an almost horizontal line will surely lead to a more nicely ordered layout: so we have now to apply a counterclockwise rotation of about 25.0 degrees.Thanks to Affine Transformations, we can combine both the previous translation and the current rotation into a single movement (a so called rototranslation). We simply have to execute the following SQL statement: CREATE TABLE sicilia_2 AS
SELECT cod_reg,
ATM_Transform(geometry,
ATM_Translate(-150000, 150000,
ATM_Translate(cx, cy,
ATM_Rotate(25,
ATM_CreateTranslate(-cx, -cy))))) AS geom
FROM (SELECT cod_reg, ST_X(centroid) AS cx, ST_Y(centroid) AS cy, geometry
FROM (SELECT cod_reg, ST_Centroid(geometry) AS centroid, geometry
FROM sicilia_0) AS g1
) AS g2;
SELECT RecoverGeometryColumn('sicilia_2', 'geom', 32632, 'MULTIPOLYGON', 'XY');
Remarks:
|
|
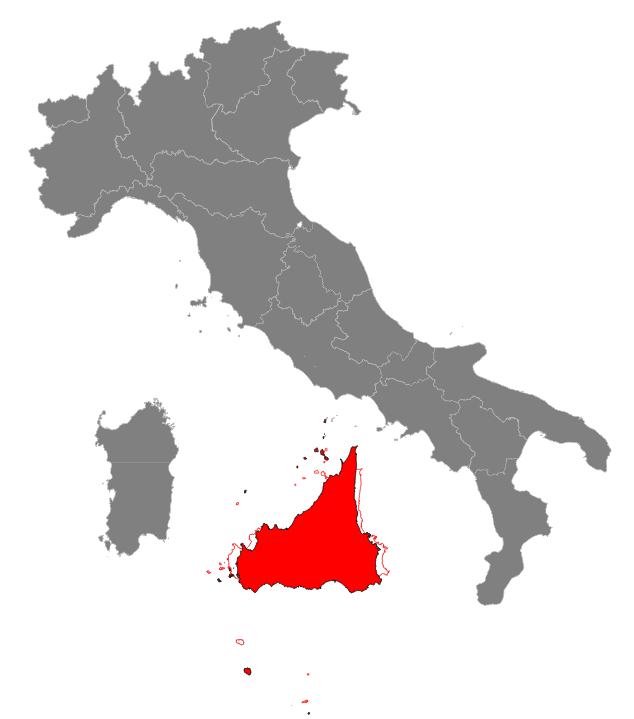
Step #3: inflating and reshaping SicilyAn increased surface is surely welcome, because it automatically implies more agricultural lands: on the other hand shortening a little bit the length of the southern coastline will surely facilitate mobility and communications.So we'll now apply a scaling transformation using two different values: sx=0.9 and sy=1.3. Once again, Affine Transformations enable us to combine altogether both translate, rotate and scale into a single transformation. This is the corresponding SQL statement:
CREATE TABLE sicilia_3 AS
SELECT cod_reg,
ATM_Transform(geometry,
ATM_Translate(-150000, 150000,
ATM_Translate(cx, cy,
ATM_Scale(0.9, 1.3,
ATM_Rotate(25,
ATM_CreateTranslate(-cx, -cy)))))) AS geom
FROM (SELECT cod_reg, ST_X(centroid) AS cx, ST_Y(centroid) AS cy, geometry
FROM (SELECT cod_reg, ST_Centroid(geometry) AS centroid, geometry
FROM sicilia_0) AS g1
) AS g2;
SELECT RecoverGeometryColumn('sicilia_3', 'geom', 32632, 'MULTIPOLYGON', 'XY');
Remarks:
|
|
Step #4: final touch: reflecting SicilyA reflected Sicily presents many interesting advantages: we'll examine all them in full detail in our study conclusions.So we'll now apply a final <a href=http://en.wikipedia.org/wiki/Reflection_%28mathematics%29">reflection transformation; this simply corresponds to a 180 degrees rotation around the Y axis. And the following is the final SQL statement applying all the above transformations in a single shot: CREATE TABLE sicilia_2 AS
CREATE TABLE sicilia_4 AS
SELECT cod_reg,
ATM_Transform(geometry,
ATM_Translate(-150000, 150000,
ATM_Translate(cx, cy,
ATM_YRoll(180,
ATM_Scale(0.9, 1.3,
ATM_Rotate(25,
ATM_CreateTranslate(-cx, -cy))))))) AS geom
FROM (SELECT cod_reg, ST_X(centroid) AS cx, ST_Y(centroid) AS cy, geometry
FROM (SELECT cod_reg, ST_Centroid(geometry) AS centroid, geometry
FROM sicilia_0) AS g1
) AS g2;
SELECT RecoverGeometryColumn('sicilia_4', 'geom', 32632, 'MULTIPOLYGON', 'XY');
Remarks:
|
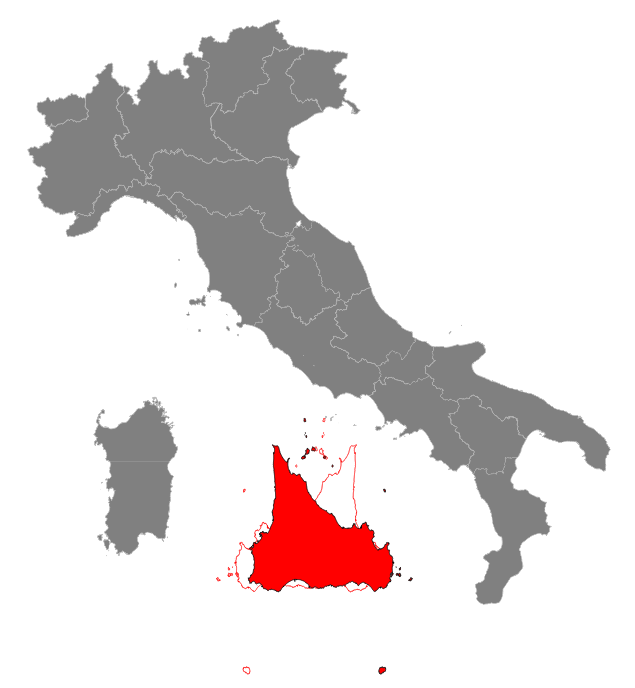
|
Final considerations
|
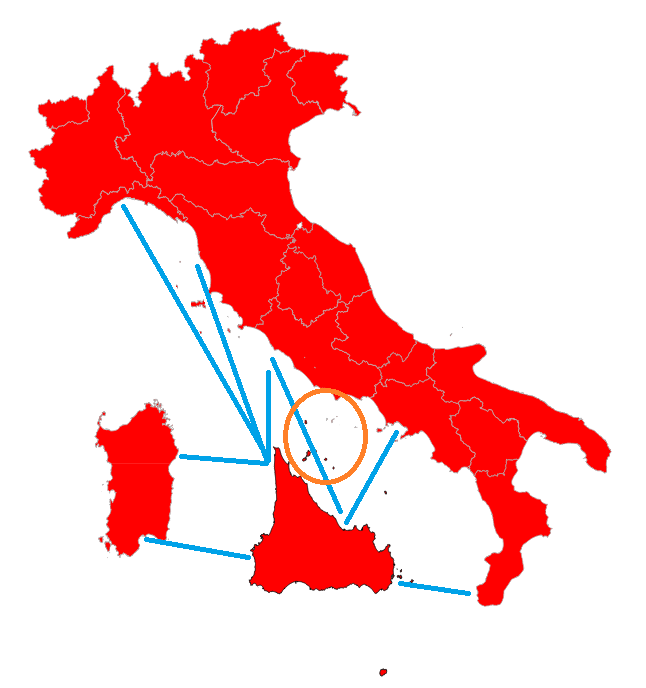
|
Boring Math: a more formal presentation
Playtime's over: we'll now start a most serious exlanation.An Affine Transformation can be represented in the form of a square matrix; the simpler 2D case requires a 3 x 3 matrix, and the followings are the possible arrangements corresponding to each elementary transformation:
| General layout | / | a | b | xoff | \ |
| | | d | e | yoff | | | |
| \ | 0 | 0 | 1 | / | |
| Identity | / | 1 | 0 | 0 | \ |
| | | 0 | 1 | 0 | | | |
| \ | 0 | 0 | 1 | / | |
| Translate(tx, ty) | / | 1 | 0 | tx | \ |
| | | 0 | 1 | ty | | | |
| \ | 0 | 0 | 1 | / | |
| Scale(sx, sy) | / | sx | 0 | 0 | \ |
| | | 0 | sy | 0 | | | |
| \ | 0 | 0 | 1 | / | |
| Rotate(θ) | / | cos(θ) | -sin(θ) | 0 | \ |
| | | sin(θ) | cos(θ) | 0 | | | |
| \ | 0 | 0 | 1 | / | |
A 3D affine transformation requires a 4 x 4 matrix.
As you can easily notice there is direct relation beetween a 3D matrix and a 2D matrix; notice the cells showing a gray backgroud.
| General layout | / | a | b | c | xoff | \ |
| | | d | e | f | yoff | | | |
| | | g | h | i | zoff | | | |
| \ | 0 | 0 | 0 | 1 | / | |
| Identity | / | 1 | 0 | 0 | 0 | \ |
| | | 0 | 1 | 0 | 0 | | | |
| \ | 0 | 0 | 1 | 0 | / | |
| \ | 0 | 0 | 0 | 1 | / | |
| Translate(tx, ty, tz) | / | 1 | 0 | 0 | tx | \ |
| | | 0 | 1 | 0 | ty | | | |
| | | 0 | 0 | 1 | tz | | | |
| \ | 0 | 0 | 0 | 1 | / | |
| Scale(sx, sy, sz) | / | sx | 0 | 0 | 0 | \ |
| | | 0 | sy | 0 | 0 | | | |
| | | 0 | 0 | sz | 0 | | | |
| \ | 0 | 0 | 0 | 1 | / | |
| X Roll(θ) | / | 1 | 0 | 0 | 0 | \ |
| | | 0 | cos(θ) | -sin(θ) | 0 | | | |
| | | 0 | sin(θ) | cos(θ) | 0 | | | |
| \ | 0 | 0 | 0 | 1 | / | |
| Y Roll(θ) | / | cos(θ) | 0 | sin(θ) | 0 | \ |
| | | 0 | 1 | 0 | 0 | | | |
| | | -sin(θ) | 0 | cos(θ) | 0 | | | |
| \ | 0 | 0 | 0 | 1 | / | |
| Z Roll(θ) | / | cos(θ) | -sin(θ) | 0 | 0 | \ |
| | | sin(θ) | cos(θ) | 0 | 0 | | | |
| | | 0 | 0 | 1 | 0 | | | |
| \ | 0 | 0 | 0 | 1 | / | |
applying an Affine Transformation
In order to materialize an affine transformation we simply have to compute (x', y', z') coordinates starting from (x, y, z) for every point or vertex found in the input Geometry accordingly to the following formulae:- x' = a*x + b*y + c*z + xoff
- y' = d*x + e*y + f*z + yoff
- z' = g*x + h*y + i*z + zoff
in the simpler 2D case this will assume the reduced form:
- x' = a*x + b*y + xoff
- y' = d*x + e*y + yoff
As you can notice, applying an Affine Transformation does not requires computing any trigonometric function.
Trigonometric functions are very costly in computational terms, so applying an Affine Transformation is an intrinsically efficient mechanism because simply depends on multiplications and additions.
chaining two (or even more) Affine Transformations in a sigle operation
Affine transformation matrices have another amazing property.We can multiply two different affine transformation matrices thus obtaining a third affine transformation matrix, and this latest once applied will contain both transformations and in the right sequence.
There is no limit; we can infinitively chain as many transformations as required, we'll simply have to continue multiplying all matrices one after the other carefully respecting the appropriate sequence.
At the end of the process we'll always get just a single affine transformation matrix faithfully representing any individual transformation in the chain.
| The multiplication between two matrices is not a commutative operation: the relative order of operands is absolutely relevant. |
multiplying two matrices
Multiplication is not really a simple operation when matrices are involved and requires a rather complex procedure; the following example show how to multiply two 4 x 4 matrices.
| * |
|
= |
|
identity matrix
An indentiy matrix simply corresponds to an affine transformation lacking any actual effect: at the end of the process the transformed geometry will be exactly the same as before.Moreover an identity matrix plays a special role in multiplication: the resulting matrix will always be exactly the same of the other matrix.
(it's more or less the equivalent of multiplying e.g. 8*1=8 in ordinary multiplication).
back