Many hyperlinks are disabled.
Use anonymous login
to enable hyperlinks.
Overview
| Artifact ID: | 5e38c649dd49d6980ce30dd87f760c54cd32c201 |
|---|---|
| Page Name: | VirtualRouting |
| Date: | 2019-12-26 16:00:19 |
| Original User: | sandro |
| Parent: | 66bbe878ad3e27e59195123329ae664085d1eddd (diff) |
Content
Back to 5.0.0-doc main page
Table of Contents
1 - Introduction2 - The sample/test DB
3 - Creating VirtualRouting Tables
4 - Solving classic Shortest Path problems
5 - Solving multi-destination Shortest Path problems
6 - Solving Isochrone problems
7 - Solving TSP (traveling salesman) problems
8 - Solving Point-to-Point problems
1 - Introduction
Previous versions of SpatiaLite traditionally supported a pure SQL routing module that was named VirtualNetwork.Since version 5.0.0 a brand new routing module (more advanced and sophisticated) is available, that is called VirtualRouting.
The now obsolete VirtualNetwork is still supported by version 5.0.0 so as to not cause an abrupt break to already existing applications, but will presumably be discontinued in future versions.
Using VirtualRouting instead of VirtualNetwirk is warmly recommended for any new development.
Theoretical foundations - an ultra-quick recall
All Routing algorithms (aka Shortest Path algorithms) are based on the mathematics of the Graph theory or to be more precise: on Weighted Graphs.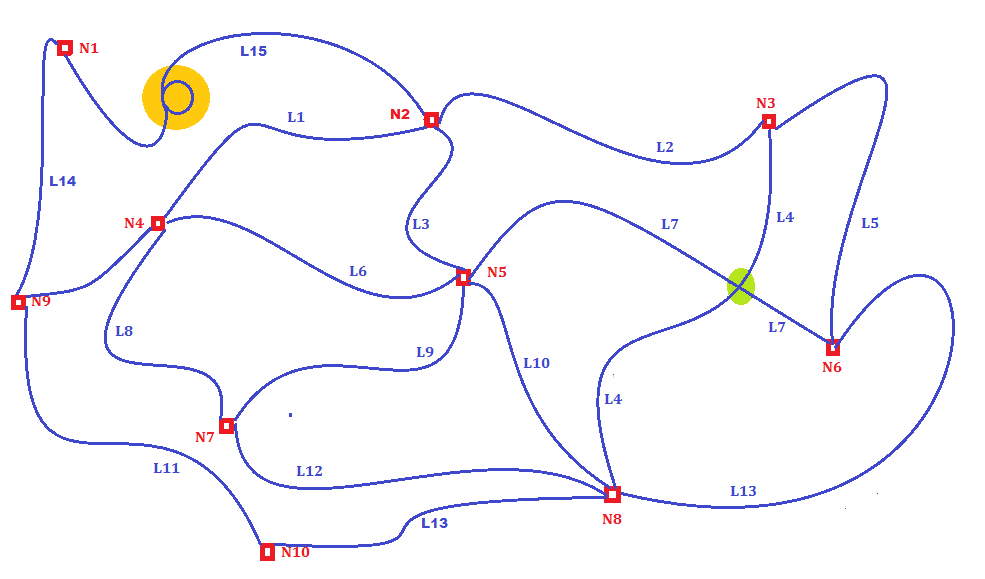
A topologically valid Network is a dataset that fulfills the following requirements:
- All items in the dataset are called Links (aka Arcs), and are expected to represent some oriented connection joining two Nodes.
Example: in the above figure Link L3 connects Nodes N2 and N5. - Therefore all Links are always expected to explicitly reference a Start-Node (aka Node-From) and an End-Node (aka Node-To).
- Links are always oriented, and their natural direction is From-To:
- in an unidirectional Network each Link is an one-way connection.
If the connection is to be available in the opposite direction, a second Link must be explicitly declared.
Example: Link X1 goes from Node A to Node B, and Link X2 goes from Node B to Node A. - in a bidirectional Network all Links are assumed to establish a connection in both directions.
Definiting an one-way connection requires an appropriate attribute to be set (see below).
- in an unidirectional Network each Link is an one-way connection.
- The Start- and End-Node could eventually be the same, and in this case we'll have a self-closed Link.
- Network's Links can eventually define a linear Geometry (LINESTRING) going from the Start-Node to the End-Node, but this is an optional feature, not a mandatory requirement.
- What is absolutely required is that each Link must explicitly reference its Nodes.
- Links are always oriented, and their natural direction is From-To:
- A Network supporting Geometries is a Spatial Network; otherwise a Network lacking any Geometry is a Logical Network.
- In a Spatial Network all Links must have a corresponding Geometry.
- In a Logical Network all Links are strictly forbidden to have any Geometry.
- In a Spatial Network both the StartPoint and EndPoint of each Link's LINESTRING are always expected to exactly coincide with the corresponding Nodes.
- In a Spatial Network all references to the same Node by different Links must be an exact match.
Example: Node N5 is shared by Links L3, L6, L7, L9 and L10, so all their corresponding LINESTRINGS are expected to have the corresponding extremity (Start- or End-, depending on the orientation) points that must exactly match the other.
A topological inconsistency exists if any of these conditions are not satisfied, which leads to an invalid Network. - Accordingly to the above premises, Nodes are never expected to be explicitly declared in a separate Table.
Just a single Table declaring all Links is required in order to fully define a topologically valid Network.
All the Nodes can then be easily extracted from the Link's definitions and the coordinates for each Node can be directly set by extracting the extreme Point of the corresponding Linestrings.
If any mismatch is detected the Network will become invalid. - A Link may legitimately self-intersect itself (e.g. forming a loop), as shown in the above figure by Link L15 (orange spot).
- Two Links may legitimately intersect where no Node exists, as exemplified on the above figure by Links L4 and L7 (green spot).
This usually happens when one of the two Links overpasses the other, or where some technical restriction exists (e.g. two insulated wires in an Electrical Network). - Links aren't strictly required to be associated with any specific attribute, but the following attributes are almost universally supported:
- a name identifying the Link.
Examples: the road toponym in a road network, or the river name in an hydrographic network. - one (or even more) appropriate cost value(s).
Example: the time required to traverse the Link (may be distinguished between pedestrians, bicycles, cars, lorries and so on). - a pair of boolean flags (from-to and to-from) are intended to specify if the Link can be traversed on both directions or just in one (one-way).
- a name identifying the Link.
- Special case: a forbidden Link is any perfectly valid Link that for any good reason can never be traversed in both directions. Practical examples:
- Road Networks: it could be useful representing pedestrian streets and bicycle lanes, but the corresponding Links will be always forbidden to car circulation.
- Telcom / Electrical Networks: several Links (wires) could be physically installed but temporarily out-of-service for technical reasons.
Logical conclusions
Any topologically valid Network (irrespective of whether it is a Spatial or Logical type) is a valid Graph.A Network allowing the support (direct or indirect) of some appropriate cost value is a valid Weighted Graph, and can consequently support Routing algorithms.
All Routing algorithms are intended to identify the Shortest Path solution connecting two Nodes in a weighted graph (aka Network).
Note: the term Shortest Path can be easily misunderstood.
Due to historical reasons the most common application field for Routing algorithms is related to Road Networks, but also many other kinds of Networks exist:
- Hydrographic Networks.
- Gas / Water / Oil Networks.
- Electrical Networks.
- Telecomunication Networks.
- Social or Economical Networks representing relationships between individuals or companies.
- Epidemiological Networks representing the propagation of infective diseases between individuals or groups.
In all the above cases we certainly have valid Networks supporting Routing algorithns, but not all of them can imply something like a spatial distance (geometric length) or a travel time.
In the most general acception costs can be represented by any reasonable physical quantity.
So a more generalized definition is assuming that Routing algorithms are intended to identify lesser cost solutions on a weighted graph.
The exact interpretation of the involved costs (aka weights) strictly depends on the very specific nature of each Network.
The Dijkstra's algorithm
This well known algorithm isn't necessarily the fastest one, but it always ensures full correctness:- Any Node-to-Node connection identified by Dijkstra's is certainly ensured to be optimal.
In other words, no connection presenting a lower cost can conceptually exist. - When Dijsjtra's fails to identify a solution this surely means that no solution is possible.
The A* algorithm
Many alternative Routing algorithms have been invented during the years.All them are based on heuristic assumptions and are intended to be faster than Dijkstra's, but none of them can ensure full correctness as Dijkstra's does.
The A* algorithm applies a mild heuristic optimization, and can be a realistic alternative to Dijkstra's in many cases.
2 - The sample/test DB
You are expected to follow the current tutorial about VirtualRouting by directly testing all SQL queries discussed below with the sample/test DB that you can download from hereThe sample DB contains the full road network of Tuscany Region (Italy) (Iter.Net dataset) kindly released under the CC-BY-SA 4.0 licence terms.
Allthough the contents stored in the sample database have been rearranged, it is still subject to the initial CC-BY-SA 4.0 clauses (derived work).
- all road names are stored within the toponyms Table.
since the same road names could be used in different Municipalities, the toponyms Table relationally references the municipalities Table (via PRIMARY / FOREIGN KEY relationships). - the roads Spatial Table contains about 380,000 Links, and has the following columns:
- id: unique identifier of each Link (PRIMARY KEY).
- node_from and node_to: Node identifiers. The original Iter.Net dataset adopts very long an complex alphanumeric Node codes; the integer Node IDs were obtained by calling the CreateRoutingNodes() SQL function discussed in a following section.
- id_toponym: relational reference to the corresponding road name contained into the toponyms Table (FOREIGN KEY).
- speed_kmh: the estimated average speed supported by the Link, expressed in km/h.
Note: negative speeds intend a forbidden Link (as it could be the case of pedestrian streets or bicycle lanes exluding motor vehicles). - oneway_fromto and oneway_tofrom: boolean flags determine if a Link can be traversed in both directions or just in a single direction (one-way).
Note: all Links declaring oneway_fromto=0 and oneway_tofrom=0 are intended to be always forbidden. - cost: the time expressed in seconds required to traverse each Link.
Note #1 all costs were calculated accordingly to the following formula: cost = ((ST_Length(geom) / 1000.0) / speed_kmh) * 3600.0
Note #2 all 86,400.0 cost values (equivalent to 1 day) imply an infinitive cost thus intending a forbidden Link. - geom: a 3D Linestring representing the Geometry of each Link.
Note: the original Iter.Net dataset is just 2D; elevations (Z coordinates) were interpolated by draping the dataset over an orographic DEM (10m X 10m cells)
- the roads_vw Spatial View resolves all relational references between roads, toponyms and municipalities, thus allowing for easier SQL queries.
- the house_nr Spatial Table contains about 1,480,000 House Numbers, and has the following columns:
- id: unique identifier of each House Number (PRIMARY KEY).
- id_road: relational reference to the corresponding Link contained into the roads Table (FOREIGN KEY).
- label: the textual label fully qualifying each House Number.
- geom: a 3D Point representing the Geometry of each House Number.
Note #1: also in this case all elevations (Z coordinates) were interpolated by draping the dataset over the same DEM as above.
Note #2: strictly speacking the House Numbers are not part of the Road Network; they are included in the sample/test database as useful examples explained later in this text.
- the house_nr_vw Spatial View resolves all relational references between house_nr, roads, toponyms and municipalities, thus allowing for easier SQL queries.
3 - Creating VirtualRouting Tables
All VirtualRouting queries are based on a specific VirtualRouting-Table, and in turn, the VirtualRouting-Table is based on a corresponding BinaryData-Table which, taken togeather, is an efficient representation of the underlying Network.So we'll start first by creating these tables.
The old, and now superseded, VirtualNetwork required the use of a separate CLI tool (spatialite_network) in order to properly initialize a VirtualNetwork Table and its companion BinaryData-Table; alternatively spatialite_gui supported a GUI wizard for the same task. Since version 5.0.0, SpatiaLite supports this functionality directly, with the CreateRouting() SQL function.
SELECT CreateRouting('byfoot_data', 'byfoot', 'roads_vw', 'node_from', 'nodeto', 'geom', NULL);
SELECT CreateRouting_GetLastError();
------------------------------------
ToNode Column "nodeto" is not defined in the Input Table
Note: this first query (based on the minimal form of CreateRouting) deliberately contains an error causing a failure that will raise an exception.CreateRouting() can fail for multiple reasons, and by calling CreateRouting_GetLastError() you can easily identify the exact reason why the most recent call to CreateRouting() failed.
SELECT CreateRouting('byfoot_data', 'byfoot', 'roads_vw', 'node_from', 'node_to', 'geom', NULL, 'toponym', 1, 1);
-------------
1
SELECT CreateRouting_GetLastError();
------------------------------------
NULL
This second attempt will succeed, with CreateRouting() returning 1 (aka TRUE), and as you can easily check now the Database contains two new Tables: byfoot and byfoot_data.Note: after a successful call to CreateRouting() CreateRouting_GetLastError() will always return NULL.
Let's look, in more detail, of the minimal form of CreateRouting(); and the meaning of each argument:
- byfoot_data: the name of the Network BinaryData-Table to be created.
- byfoot: the name of the VirtualRouting-Table to be created.
- roads_vw: the name of the Spatial Table or Spatial View representing the underlying Network.
Note: in this case we actually used a Spatial View. - node_from: name of the column (in the above Table or View) expected to contain node-from values.
- node_to: name of the column (in the above Table or View) expected to contain node-to values.
- geom: name of the column (in the above Table or View) expected to contain Linestrings.
In the case of a Logical Network: a NULL should be passed.. - NULL: name of the column (in the above Table or View) expected to contain cost values.
In this case we have passed a NULL value, and consequently the cost of each Link will be assumed to be represented by the geometric length of the corresponding Linestring.
Note #1: in the case of Networks based on longitudes and latitudes (aka geographic Reference Systems) the geometry length of all Linestrings will be precisely measured on the ellipsoid by applying the most accurate geodesic formulas and will consequently be expressed in meters. In any other case (projected Reference Systems) lengths will be expressed in the measure unit defined by the Reference System (e.g. meters for UTM projections and feet for NAD-ft projections).
Note #2: the geom-column and cost-column arguments are never allowed to be NULL at the same time. - toponym: name of the column (in the above Table or View) expected to contain road-name values.
It could be legitimately set to NULL if all Links are anonymous. - 1: a boolean flag intended to specify if the Network must support the A* algorithm or not (set to TRUE by default).
- 1: a boolean flag intended to specify if all Network's Links are assumed to be bidirectional or not (assumed to be TRUE by default).
Technical noteThe internal encoding adopted by the BinaryData-Table is unchanged and is the same for both VirtualNetwok and VirtualRouting.You can safely base a VirtualRouting-Table on any existing BinaryData-Table created by the spatialite-network CLI tool, exactly as you can base a VirtualNetwork Table on any BinaryData-Table created by the CreateRouting() SQL function.
CREATE VIRTUAL TABLE test_network USING VirtualNetwork('some_data_table');
CREATE VIRTUAL TABLE test_routing USING VirtualRouting('some_data_table');
In order to manually create your Virtual Tables you just have to execute an appropriate CREATE VIRTUAL TABLE ... USING Virtual... (...) statement.
WarningIn the case of Spatial Networks based on any geographic Reference System (using longitudes and latitudes) there is an important difference between BinaryData-Tables created by the spatialite_network GUI tool and BinaryData-Tables created by the CreateRouting() SQL function when costs are implicitly based on the geometric length of the Link's Linestring:
|
SELECT CreateRouting('bycar_data', 'bycar', 'roads_vw', 'node_from', 'node_to', 'geom', 'cost', 'toponym', 1, 1, 'oneway_fromto', 'oneway_tofrom', 0);
--------------------
1
After calling CreateRouting() correctly, the Database contains two further Tables: bycar and bycar_data.This time you've used the complete form of CreateRouting(); let's see in more depth all the arguments and their meaning:
- bycar_data: same as above.
- bycar: same as above.
- roads_vw: same as above.
- node_from: same as above.
- node_to: same as above.
- geom: same as above.
- cost: same as above. In this case we have referenced a column preloaded with values corresponding to the time measured in seconds required to traverse each Link.
- toponym: same as above.
- 1: same as above (A* enabled).
- 1: same as above (bidirectional Links).
- oneway_fromto: name of the column (in the above Table or View) expected to contain boolean flags specifying if each Link can be traversed in the from-to direction or not.
- oneway_tofrom: name of the column (in the above Table or View) expected to contain boolean flags specifying if each Link can be traversed in the to-from direction or not.
Note #1: both from-to and to-from column names can be legitimately set as NULL if no one-way restrictions apply to the current Network.
Note #2: Networks of the unidirectional type are never enabled to reference one-way columns (they should always be set to NULL). - 0: a boolean flag specifying an overwrite authorization.
- If set to FALSE an exception will be raised if the BinaryData-Table and/or the VirtualRouting-Table already exist.
- If set to TRUE eventually existing Tables will be, to avoid errors, dropped before starting the execution of CreateRouting().
Highlight: where you areYou've just created two VirtualRouting-Tables based on different settings; both them are perfectly valid and reasonable, but they are intended for different purposes:
Conclusion: a single VirtualRouting-Table cannot adequately support all requirements and expectations of different users. Defining more Routing Tables with different settings for the same Network usually is a good design choice leading to more realistic results. |
Utility function for automatically setting NodeFrom and NodeTo IDs
It could happen that a Spatial Network representation is topologically consistent, but completely lacking of any NodeFrom and NodeTo definitions.In such a case you can successfully rebuild the missing NodeFrom and NodeTo definitions from a valid Network by calling the CreateRoutingNodes() SQL function.
SELECT CreateRoutingNodes(NULL, 'table_name', 'geom', 'node_from', 'node_to'); _________________________ 1Let's examine all arguments and their meanings:
- NULL: name of the Attached-DB containing the Spatial Table.
It can be legitimately set to NULL, and in this case the MAIN DB is assumed. - table_name: name of the Spatial Table.
- geom : name of the column (in the above Table) containing Linestrings.
- node_from: name of the column to be added to the above Table and populated with appropriate NodeFrom IDs.
- node_to: name of the column to be added to the above Table and populated with appropriate NodeTo IDs.
Note: both NodeFrom and NodeTo columns should not be already defined in the above Table.
Note: you can call CreateRouting_GetLastError() so to precisely identify the cause accounting for failure.
Handling dynamic NetworksA Network could be subject to rather frequent changes, such as:
A VirtualRouting-Table is always based on a companion BinaryData-Table, that is intrinsically static, and consequently you are required to re-create both of them from time to time in order to support all recent changes affecting the underlaying Network. The optimal frequency for the refreshing of the the Routing Tables depends strictly on the specific requirements, but these two overall approaches are commonly adopted:
|
Warning: how to correctly drop Network TablesWhen dropping a VirtualRouting-Table and its companion BinaryData-Table strictly respecting the correct sequence of SQL commands is essential.Failing to strictly respect this expected sequence will surely cause you several troubles and severe headaches, and will possibly lead to a completely corrupted database..
|
4 - Solving classic Shortest Path problems
The most classic Shortest Path problem requires to identify the optimal connection between an Origin Node and a Destination Node.We can easily translate such a problem into a simple SQL query targeting some VirtualRouting-Table.
SELECT * FROM byfoot WHERE NodeFrom = 178731 AND NodeTo = 183286;
| Algorithm | Request | Options | Delimiter | RouteId | RouteRow | Role | LinkRowid | NodeFrom | NodeTo | PointFrom | PointTo | Tolerance | Cost | Geometry | Name |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Dijkstra | Shortest Path | Full | , [dec=44, hex=2c] | 0 | 0 | Route | NULL | 178731 | 183286 | NULL | NULL | NULL | 300.912208 | BLOB sz=272 GEOMETRY | NULL |
| NULL | NULL | NULL | NULL | 0 | 1 | Link | 224014 | 178731 | 182885 | NULL | NULL | NULL | 94.812424 | NULL | VIA PIETRO ARETINO |
| NULL | NULL | NULL | NULL | 0 | 2 | Link | 224446 | 182885 | 178880 | NULL | NULL | NULL | 69.727726 | NULL | VIA MARGARITONE |
| NULL | NULL | NULL | NULL | 0 | 3 | Link | 224414 | 178880 | 183286 | NULL | NULL | NULL | 136.372057 | NULL | VIA MARGARITONE |
Let's quickly examine the resultset returned by the above Routing query:
- the first row (aka header row) has a special interpretation, and is intended to summarize the travel solution as a whole.
- all the following rows represent a single Link required to build the solution (optima path); Links are ordered accordingly to the travel direction connecting the Origin and the Destination.
- columns Algorithm, Request, Options, Delimiter, PointFrom, PointTo, Tolerance and Geometry are always set to NULL (except that of the first row of the resultset):
- column Algorithm accounts for the Routing Algorithm used by the current query (Dijkstra's or A*).
- column Request specifies the exact nature of the current query (in this specific case Shortest Path).
- for now we'll ignore the columns Options, Delimiter, PointFrom, PointTo and Tolerance: their respective meanings will be explained in following paragraphs.
- column Geometry contains a LINESTRING representation of the whole Route solution.
Note: on Logical Networks (not supporting Geometries) Geometry will always be NULL.
- we'll ignore for now column RouteId; its meaning will be explained in following paragraphs.
- column RouteRow simply is the progressive number of the row in the travel solution (always 0 in the header row).
- column Role can be Route (header row) or Link (all following rows).
- column LinkRowid references the ROWID of the corresponding Link (always set to NULL in the header row).
- column NodeFrom and NodeTo have the following interpretation:
- in the header row they correspond to he Origin and Destination Nodes.
- in all of the following rows they are intended to specify the direction of the current Link.
- column Cost has the following interpretation:
- in the header row it corresponds to the total cost of the route.
- in all of the following rows it represents the specific cost of the current Link.
- column Name contains the description of the current Link (usually a road name), and is always NULL in the header row.
Note it could be always be NULL if the VirtualRouting-Table does not supports names (i.e. the road_name_column parm of CreateRouting was not used).
Testing the return connection just requires swapping the Origin and the Destination; in this example you'll just query the needed columns:
SELECT RouteRow, Role, LinkRowid, NodeFrom, NodeTo, Cost, Geometry, Name FROM byfoot WHERE NodeTo = 178731 AND NodeFrom = 183286;
| RouteRow | Role | LinkRowid | NodeFrom | NodeTo | Cost | Geometry | Name |
|---|---|---|---|---|---|---|---|
| 0 | Route | NULL | 183286 | 178731 | 300.912208 | BLOB sz=272 GEOMETRY | NULL |
| 1 | Link | 224414 | 183286 | 178880 | 136.372057 | NULL | VIA MARGARITONE |
| 2 | Link | 224446 | 178880 | 182885 | 69.727726 | NULL | VIA MARGARITONE |
| 3 | Link | 224014 | 182885 | 178731 | 94.812424 | NULL | VIA PIETRO ARETINO |
As you'll remember, the byfoot VirtualRouting-Table has no one-ways, and consequently the return path corresponds to the first one, except in that all directions are now reversed.
Now you'll test the same connections, but this time you'll target the bycar VirtualRouting-Table that fully supports one-ways:
SELECT RouteRow, Role, LinkRowid, NodeFrom, NodeTo, Cost, Geometry, Name FROM bycar WHERE NodeFrom = 178731 AND NodeTo = 183286;
| RouteRow | Role | LinkRowid | NodeFrom | NodeTo | Cost | Geometry | Name |
|---|---|---|---|---|---|---|---|
| 0 | Route | NULL | 178731 | 183286 | 101.815552 | BLOB sz=2032 GEOMETRY | NULL |
| 1 | Link | 224014 | 178731 | 182885 | 13.127874 | NULL | VIA PIETRO ARETINO |
| 2 | Link | 224446 | 182885 | 178880 | 9.654608 | NULL | VIA MARGARITONE |
| 3 | Link | 219171 | 178880 | 178732 | 7.809952 | NULL | VIA FRANCESCO CRISPI |
| 4 | Link | 219058 | 178732 | 178754 | 12.445626 | NULL | VIA FRANCESCO CRISPI |
| 5 | Link | 225888 | 178754 | 183461 | 1.599865 | NULL | VIA FRANCESCO CRISPI |
| 6 | Link | 225887 | 183461 | 182800 | 3.300590 | NULL | VIA FRANCESCO CRISPI |
| 7 | Link | 223935 | 182800 | 182799 | 6.688786 | NULL | VIALE LUCA SIGNORELLI |
| 8 | Link | 226038 | 182799 | 183456 | 1.294017 | NULL | VIALE LUCA SIGNORELLI |
| 9 | Link | 225832 | 183456 | 183444 | 2.385486 | NULL | VIALE LUCA SIGNORELLI |
| 10 | Link | 225831 | 183444 | 183554 | 3.160662 | NULL | VIALE LUCA SIGNORELLI |
| 11 | Link | 225765 | 183554 | 183954 | 7.469917 | NULL | VIALE LUCA SIGNORELLI |
| 12 | Link | 225766 | 183954 | 183905 | 3.236389 | NULL | VIALE LUCA SIGNORELLI |
| 13 | Link | 225979 | 183905 | 183626 | 13.983629 | NULL | STRADA SENZA NOME |
| 14 | Link | 224905 | 183626 | 183128 | 5.627358 | NULL | STRADA SENZA NOME |
| 15 | Link | 224897 | 183128 | 183286 | 10.030792 | NULL | VIA MARGARITONE |
SELECT RouteRow, Role, LinkRowid, NodeFrom, NodeTo, Cost, Geometry, Name FROM bycar WHERE NodeTo = 178731 AND NodeFrom = 183286;
| RouteRow | Role | LinkRowid | NodeFrom | NodeTo | Cost | Geometry | Name |
|---|---|---|---|---|---|---|---|
| 0 | Route | NULL | 183286 | 178731 | 103.305259 | BLOB sz=944 GEOMETRY | NULL |
| 1 | Link | 224414 | 183286 | 178880 | 18.882285 | NULL | VIA MARGARITONE |
| 2 | Link | 219171 | 178880 | 178732 | 7.809952 | NULL | VIA FRANCESCO CRISPI |
| 3 | Link | 219058 | 178732 | 178754 | 12.445626 | NULL | VIA FRANCESCO CRISPI |
| 4 | Link | 224538 | 178754 | 181972 | 7.047784 | NULL | VIA ANTONIO GUADAGNOLI |
| 5 | Link | 222575 | 181972 | 181971 | 1.852283 | NULL | VIA ANTONIO GUADAGNOLI |
| 6 | Link | 224967 | 181971 | 182891 | 14.273185 | NULL | VIA ANTONIO GUADAGNOLI |
| 7 | Link | 224168 | 182891 | 183057 | 6.643309 | NULL | VIA MACALLE' |
| 8 | Link | 224167 | 183057 | 183056 | 3.151272 | NULL | VIA MACALLE' |
| 9 | Link | 224174 | 183056 | 182941 | 7.966870 | NULL | VIA RODI |
| 10 | Link | 224059 | 182941 | 182001 | 6.393747 | NULL | VIA RODI |
| 11 | Link | 222637 | 182001 | 182000 | 2.475538 | NULL | VIA PIETRO ARETINO |
| 12 | Link | 222636 | 182000 | 178731 | 14.363408 | NULL | VIA PIETRO ARETINO |
As you can see, the optimal paths returned by the bycar VirtualRouting-Table in the opposite directions strongly differ, and both are completely different from the paths returned by querying byfoot.
A quick glance at the map below will help to understand better what's really happening.
This is a central area of the town of Arezzo around the archaeological ruins of the Roman Amphitheater; traveling by car should be avoided, due to the many one-way restrictions. Not surprisingly, going by foot is the faster option.
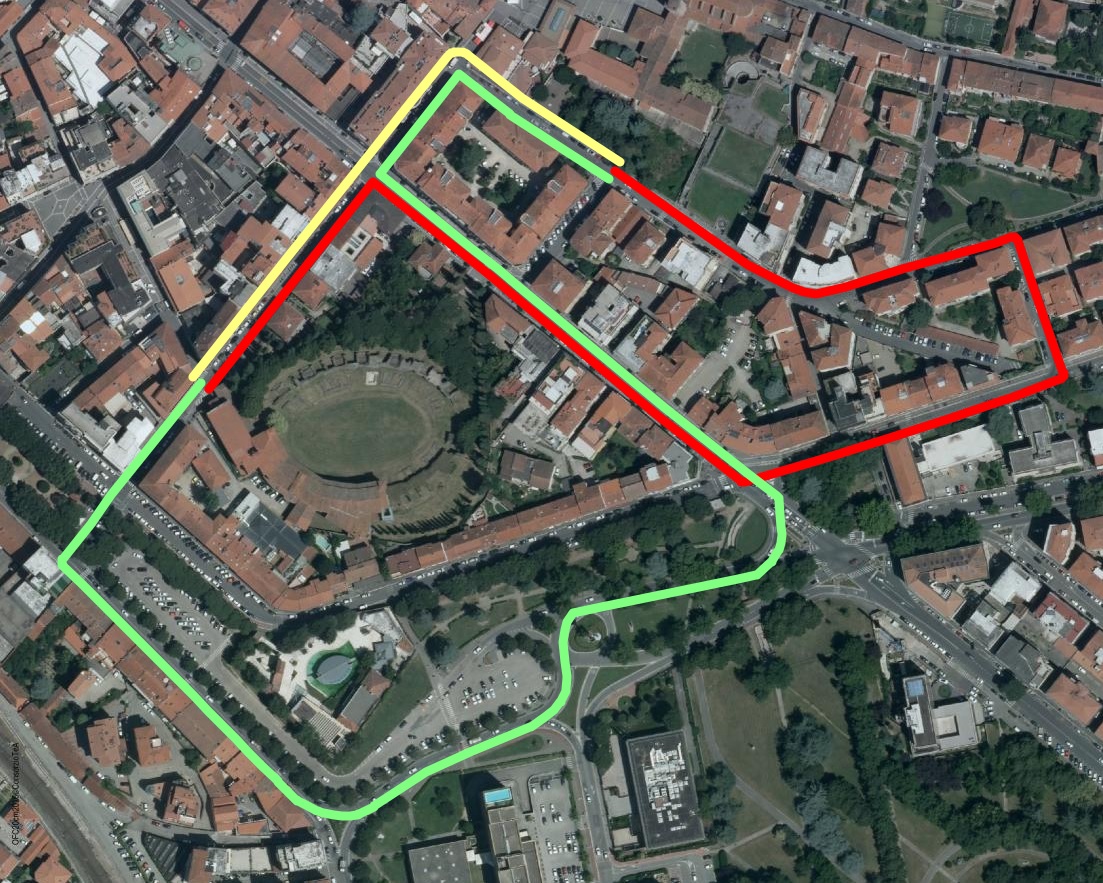
- yellow path: pedestrians
- green path: car, forward direction
- red path: car, return direction
Linestrings returned by VirtualRoutingAll LINESTRING Geometries created by any VirtualRouting will always contain M values:
In other words, all Linestrings returned by VirtualRouting can effectively support LR (Linear Referencing) SQL functions, as in the following examples: SELECT ST_Locate_Between_Measures(<geometry>, 30.0, 45.0); SELECT ST_Locate_Between_Measures(<geometry>, 80.0, 95.0);The side map graphically shows the estimated positions respectively 30-45 seconds after starting (yellow dotted line) and 80-95 seconds after starting (green dotted line). (assuming the same path returned by the latest bycar query). |
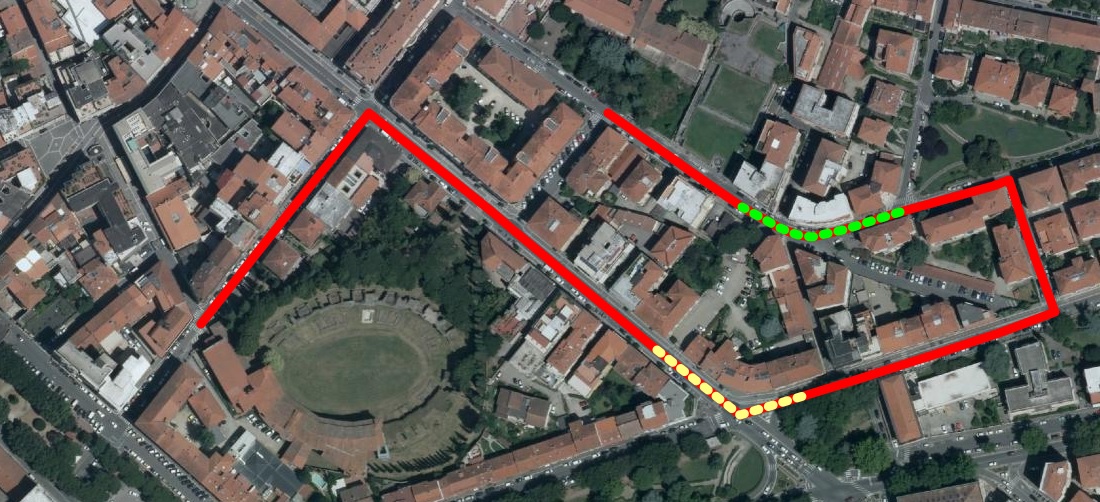 |
Playing with VirtualRouting configurable options
Several aspects of VirtualRouting can be freely customized.UPDATE byfoot SET Algorithm = 'A*'; SELECT Algorithm, Options, RouteRow, Role, LinkRowid, NodeFrom, NodeTo, Cost, Geometry, Name FROM byfoot WHERE NodeFrom = 178731 AND NodeTo = 183286;As you'll remember in all the previous examples the Dijkstra's algorithm was used; now (after executing the above UPDATE) all Shortest Path queries will be based on the alternative A* algorithm.
If you wish to switch back to the Dijkstra's algorithm you just have to execute
UPDATE byfoot SET Algorithm = 'DIJKSTRA';.
The following table shows the resultset returned by the previous Shortest Path query; please notice the value in the Algorithm column.
| Algorithm | Options | RouteRow | Role | LinkRowid | NodeFrom | NodeTo | Cost | Geometry | Name |
|---|---|---|---|---|---|---|---|---|---|
| A* | Full | 0 | Route | NULL | 178731 | 183286 | 300.912208 | BLOB sz=272 GEOMETRY | NULL |
| NULL | NULL | 1 | Link | 224014 | 178731 | 182885 | 94.812424 | NULL | VIA PIETRO ARETINO |
| NULL | NULL | 2 | Link | 224446 | 182885 | 178880 | 69.727726 | NULL | VIA MARGARITONE |
| NULL | NULL | 3 | Link | 224414 | 178880 | 183286 | 136.372057 | NULL | VIA MARGARITONE |
You can also configure the resultset returned the VirtualRouting queries.
UPDATE byfoot SET Options = 'NO LINKS'; SELECT Algorithm, Options, RouteRow, Role, LinkRowid, NodeFrom, NodeTo, Cost, Geometry, Name FROM byfoot WHERE NodeFrom = 178731 AND NodeTo = 183286;After setting Options='NO LINKS' the resultset will simply contain the header row, and all of the following rows will be suppressed.
Note: producing a reduced resultset is expected to be someway faster.
The following table shows the resultset returned by the previous Shortest Path query.
Notice that value in the Options column shows you which type of resultset you are using (just as the Algorithm column shows which algorithm is active).
| Algorithm | Options | RouteRow | Role | LinkRowid | NodeFrom | NodeTo | Cost | Geometry | Name |
|---|---|---|---|---|---|---|---|---|---|
| A* | No Links | 0 | Route | NULL | 178731 | 183286 | 300.912208 | BLOB sz=272 GEOMETRY | NULL |
UPDATE byfoot SET Options = 'NO GEOMETRIES'; SELECT Algorithm, Options, RouteRow, Role, LinkRowid, NodeFrom, NodeTo, Cost, Geometry, Name FROM byfoot WHERE NodeFrom = 178731 AND NodeTo = 183286;After setting Options='NO GEOMETRIES' the resultset will contain all rows, but all Geometries will be suppressed.
Note: this too is expected to be somewhat faster.
The following table shows the resultset returned by the previous Shortest Path query; please notice the value in the Options column.
| Algorithm | Options | RouteRow | Role | LinkRowid | NodeFrom | NodeTo | Cost | Geometry | Name |
|---|---|---|---|---|---|---|---|---|---|
| A* | No Geometries | 0 | Route | NULL | 178731 | 183286 | 300.912208 | NULL | NULL |
| NULL | NULL | 1 | Link | 224014 | 178731 | 182885 | 94.812424 | NULL | VIA PIETRO ARETINO |
| NULL | NULL | 2 | Link | 224446 | 182885 | 178880 | 69.727726 | NULL | VIA MARGARITONE |
| NULL | NULL | 3 | Link | 224414 | 178880 | 183286 | 136.372057 | NULL | VIA MARGARITONE |
UPDATE byfoot SET Options = 'SIMPLE'; SELECT Algorithm, Options, RouteRow, Role, LinkRowid, NodeFrom, NodeTo, Cost, Geometry, Name FROM byfoot WHERE NodeFrom = 178731 AND NodeTo = 183286;Setting Options='SIMPLE' has the same effect than setting both NO LINKS and NO GEOMETRIES at the same time.
Note: this is expected to be the fastest setting.
The following table shows the resultset returned by the previous Shortest Path query; please notice the value in the Options column.
| Algorithm | Options | RouteRow | Role | LinkRowid | NodeFrom | NodeTo | Cost | Geometry | Name |
|---|---|---|---|---|---|---|---|---|---|
| A* | Simple | 0 | Route | NULL | 178731 | 183286 | 300.912208 | NULL | NULL |
Finally, if you wish to revert back to the initial setting, you do this with the following query
UPDATE byfoot SET Options = 'FULL';.
5 - Solving multi-destination Shortest Path problems
An interesting feature supported by the Dijkstra's Algorithm is: when a destination is been reached, all of the lesser cost destinations have also been found.This allows the support of multiple destinations Shortest Path queries.
All you have to do is specify a single origin Node with an arbitrary list of destination Nodes in one Dijkstra's query.
Note: executing a multi-destination Shortest Path query requires a processing time that isn't the sum of all individual timings to each destination, but simply the time required to reach the most costly destination of the list.
This isn't strictly true in the case of this VirtualRouting specific implementation, since the arrangment the resultset to be returned and creation all the individual Linestrings for each destination will surely impose some further overhead.
Nevertheless the time needed for a single multi-destination query will be less than the time needed for multiple single-destination queries.
SELECT Algorithm, Request, Options, Delimiter, RouteId, RouteRow, Role, LinkRowid, NodeFrom, NodeTo, Cost, Geometry, Name FROM byfoot WHERE NodeFrom = 178731 AND NodeTo = '183286,290458,181999,184030,124622,183882,178754';As you can see, a multiple-destinations query has the same identical form of any normal Shortest Path query, the only difference being a comma-separated list (instead of a single-entry) for NodeTo.
The following table shows the resultset returned by the previous multi-destination Shortest Path query:
| Algorithm | Request | Options | Delimiter | RouteId | RouteRow | Role | LinkRowid | NodeFrom | NodeTo | Cost | Geometry | Name |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Dijkstra | Shortest Path | Full | , [dec=44, hex=2c] | 0 | 0 | Route | NULL | 178731 | 183882 | 154.750839 | BLOB sz=240 GEOMETRY | NULL |
| NULL | NULL | NULL | NULL | 0 | 1 | Link | 222636 | 178731 | 182000 | 103.735722 | NULL | VIA PIETRO ARETINO |
| NULL | NULL | NULL | NULL | 0 | 2 | Link | 225527 | 182000 | 183882 | 51.015117 | NULL | VIA LICIO NENCETTI |
| NULL | NULL | NULL | NULL | 1 | 0 | Route | NULL | 178731 | 184030 | 176.364755 | BLOB sz=304 GEOMETRY | NULL |
| NULL | NULL | NULL | NULL | 1 | 1 | Link | 224014 | 178731 | 182885 | 94.812424 | NULL | VIA PIETRO ARETINO |
| NULL | NULL | NULL | NULL | 1 | 2 | Link | 224862 | 182885 | 182043 | 37.095287 | NULL | VIA MARGARITONE |
| NULL | NULL | NULL | NULL | 1 | 3 | Link | 226070 | 182043 | 184030 | 44.457044 | NULL | PIAZZA SANT'AGOSTINO |
| NULL | NULL | NULL | NULL | 2 | 0 | Route | NULL | 178731 | 178754 | 224.677095 | BLOB sz=240 GEOMETRY | NULL |
| NULL | NULL | NULL | NULL | 2 | 1 | Link | 219045 | 178731 | 178732 | 76.021007 | NULL | VIA ASSAB |
| NULL | NULL | NULL | NULL | 2 | 2 | Link | 219058 | 178732 | 178754 | 148.656089 | NULL | VIA FRANCESCO CRISPI |
| NULL | NULL | NULL | NULL | 3 | 0 | Route | NULL | 178731 | 181999 | 260.132354 | BLOB sz=240 GEOMETRY | NULL |
| NULL | NULL | NULL | NULL | 3 | 1 | Link | 224014 | 178731 | 182885 | 94.812424 | NULL | VIA PIETRO ARETINO |
| NULL | NULL | NULL | NULL | 3 | 2 | Link | 224446 | 182885 | 178880 | 69.727726 | NULL | VIA MARGARITONE |
| NULL | NULL | NULL | NULL | 3 | 3 | Link | 225800 | 178880 | 181999 | 95.592204 | NULL | VIA FRANCESCO CRISPI |
| NULL | NULL | NULL | NULL | 4 | 0 | Route | NULL | 178731 | 183286 | 300.912208 | BLOB sz=272 GEOMETRY | NULL |
| NULL | NULL | NULL | NULL | 4 | 1 | Link | 224014 | 178731 | 182885 | 94.812424 | NULL | VIA PIETRO ARETINO |
| NULL | NULL | NULL | NULL | 4 | 2 | Link | 224446 | 182885 | 178880 | 69.727726 | NULL | VIA MARGARITONE |
| NULL | NULL | NULL | NULL | 4 | 3 | Link | 224414 | 178880 | 183286 | 136.372057 | NULL | VIA MARGARITONE |
| NULL | NULL | NULL | NULL | NULL | NULL | Unreachable NodeTo | NULL | 178731 | 290458 | NULL | NULL | NULL |
| NULL | NULL | NULL | NULL | NULL | NULL | Unreachable NodeTo | NULL | 178731 | 124622 | NULL | NULL | NULL |
Let's quickly examine the resultset returned by the above multi-destinations query.
- the overall layout is almost exactly the same as you've already seen in the case of single-destination queries, but in this case more individual travel solutions are grouped altogether. (Each alternative route having a different RouteId and starting with 'Route' in the Role column).
- the first row of the resultset is someway exceptional, and is the only row of the resultset presenting NOT NULL values in the Algorithm, Request, Options and Delimiter columns.
- the RouteId column is intended to group together all rows belonging to same travel solution (aka Route).
Routes are progressively numbered and are ordered accordingly to their total cost. - the RouteRow column has the same interpretation as in single-destination resultsets, and is intended to progressively order in the correct sequence all Links connecting the Origin and the Destination of each Route.
RouteRow=0 always identifies the header row of each Route solution.
Notice: the last two rows in the resultset reports Unreachable NodeTo in the Role column, thus implying a forbidden connection.
There is a valid reason for this: Nodes 290458 and 124622 are located on Elba and Giglio islands. The underlaying Network is based on Iter.Net that don't supports ferry connections, so any travel solution between the islands and the mainland will always fail.
Also multi-destinations queries can be customized, but the configuration rules differ slightly from what you have already seen in the case of single-destination.
- Algorithm: only Dijkstra is supported by multi-destination, and will be implicitly assumed even when the alternative A* algorithm is currently selected.
- Options: the usual FULL, SIMPLE, NO LINKS and NO GEOMETRIES are supported and will have the same effect as in single-destination queries.
UPDATE byfoot SET Options = 'SIMPLE'; SELECT Algorithm, Request, Options, Delimiter, RouteId, RouteRow, Role, LinkRowid, NodeFrom, NodeTo, Cost, Geometry, Name FROM byfoot WHERE NodeFrom = 178731 AND NodeTo = '183286,290458,181999,184030,124622,183882,178754';The following table shows the resultset returned by the same multi-destination query used in the previous example after enabling the SIMPLE option.
| Algorithm | Request | Options | Delimiter | RouteId | RouteRow | Role | LinkRowid | NodeFrom | NodeTo | Cost | Geometry | Name |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Dijkstra | Shortest Path | Full | , [dec=44, hex=2c] | 0 | 0 | Route | NULL | 178731 | 183882 | 154.750839 | NULL | NULL |
| NULL | NULL | NULL | NULL | 1 | 0 | Route | NULL | 178731 | 184030 | 176.364755 | NULL | NULL |
| NULL | NULL | NULL | NULL | 2 | 0 | Route | NULL | 178731 | 178754 | 224.677095 | NULL | NULL |
| NULL | NULL | NULL | NULL | 3 | 0 | Route | NULL | 178731 | 181999 | 260.132354 | NULL | NULL |
| NULL | NULL | NULL | NULL | 4 | 0 | Route | NULL | 178731 | 183286 | 300.912208 | NULL | NULL |
| NULL | NULL | NULL | NULL | NULL | NULL | Unreachable NodeTo | NULL | 178731 | 290458 | NULL | NULL | NULL |
| NULL | NULL | NULL | NULL | NULL | NULL | Unreachable NodeTo | NULL | 178731 | 124622 | NULL | NULL | NULL |
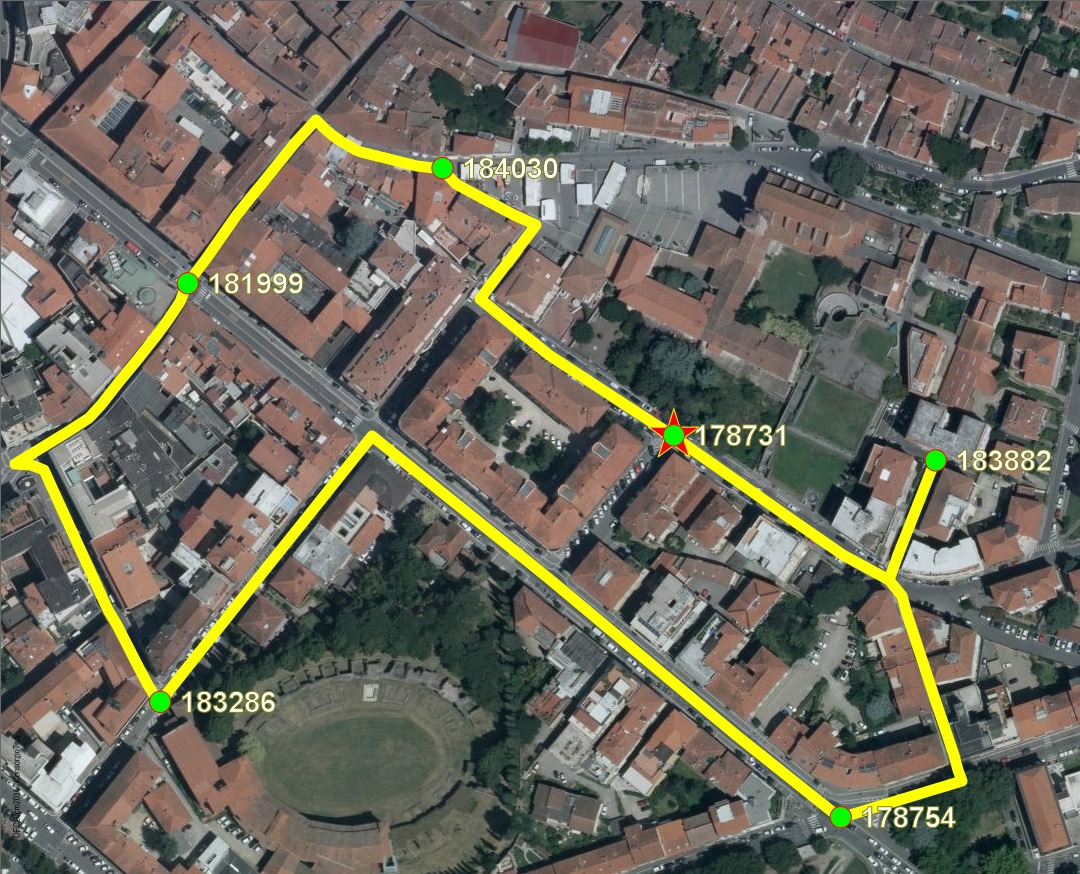
The map below graphically shows the previous multi-destinations queries.
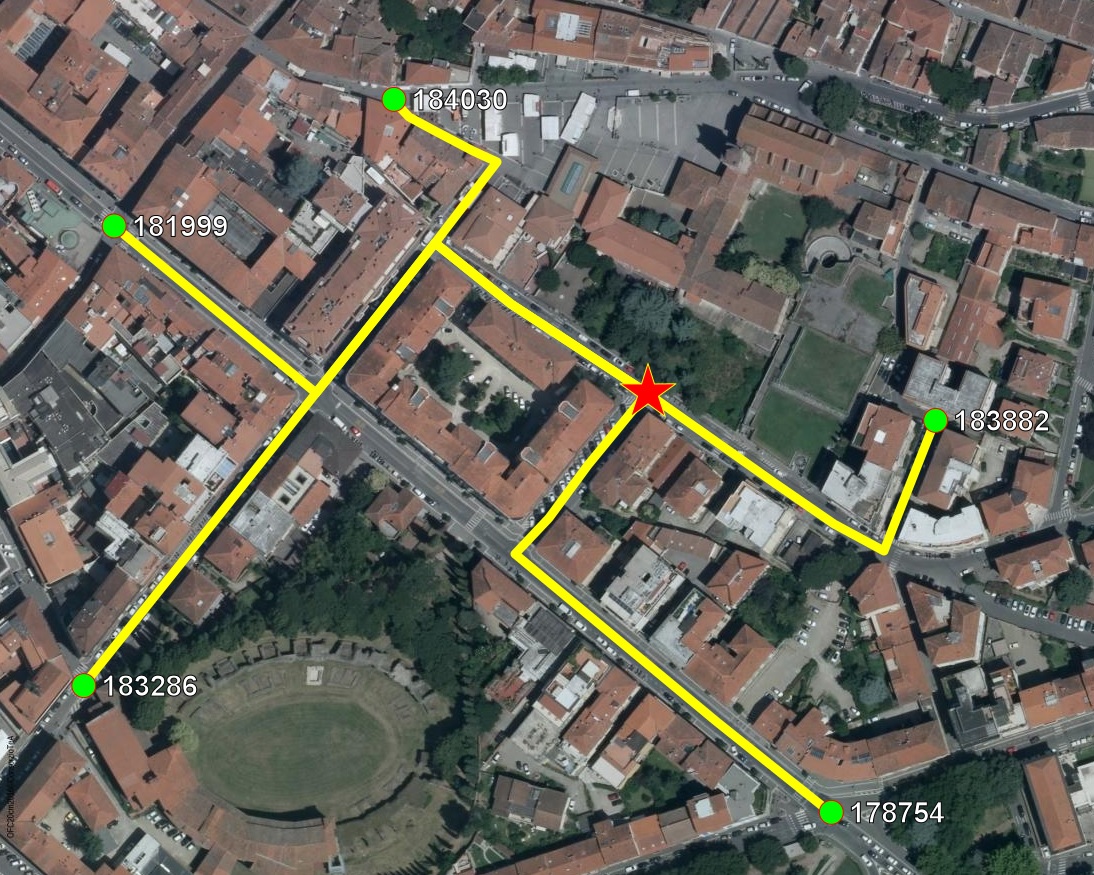
- Red star: the Origin Node.
- Green dots: the Destination Nodes.
- Yellow lines: all individual travel solutions.
Dangerous pitfalls related to multiple destination listsSQL syntax directly allows to specify lists of multiple values, so may be you are now wondering about writing the multiple destinations query tested in the previous examples this way:SELECT Algorithm, Request, Options, Delimiter, RouteId, RouteRow, Role, LinkRowid, NodeFrom, NodeTo, Cost, Geometry, Name FROM byfoot WHERE NodeFrom = 178731 AND NodeTo IN (183286, 290458, 181999, 184030, 124622, 183882, 178754);There is a very good reason to discourage you from doing such a thing, let's see why: For SQLite: NodeTo IN (183286, 290458, 181999, 184030, 124622, 183882, 178754) is considered to be 7 parameters for which VirtualRouting will be called for each. Whereas: NodeTo = '183286,290458,181999,184030,124622,183882,178754' is considered to be 1 parameter for which VirtualRouting will be called once and search for the 7 items. BewareNever ever attempt to define a list of multiple destinations using the standard SQL syntax WHERE NodeTo IN (......), because this will certainly cause many unexpected 'results'.Badly formatted resultsets will be then returned, many of which may be wrong. You are warned. |
How to correctly format multiple destinations listsVirtualRouting always expects to receive a multi-destinations list as a TEXT string containing tightly packed values separated by a conventional delimiter (usually represented by a comma).Examples of well formatted multi-destinations lists: '1,2,3,4,5,10,100,1000,100000' -- integer Node IDs 'A100B,A100F,B250Z,C010M,Z999A' -- alphanumeric Node CodesExamples of badly formatted multi-destinations lists: ' 1, 2, 3, 4 , 5 , 10, 100, 1000, 100000 ' -- integer Node IDs ' A100B, A100F , B250Z , C010M, Z999A ' -- alphanumeric Node CodesNote: all whitespaces immediately preceding or following the delimiter will be considered to be integral part of the value itself (and thus will also be searched for). This will have no adverse consequences in the case of integer values, but can easily have catastrophic effects on alphanumeric values. Defining a custom delimiterSometimes it could be useful setting up a delimiter other than a comma.UPDATE byfoot SET Delimiter = '*'; SELECT Delimiter FROM byfoot; ------------------ * [dec=42, hex=2a]You simply have to execute an UPDATE statement by specifying the new delimiter value. |
Using MakeStringList() for auto-writing a list of multiple destinations
Writing by hand a Text String corresponding to a well-formatted list of multiples destinations could easily be a boring and error prone activity (most notably if the list contains a huge number of destination Nodes).
SELECT MakeStringList(node_id)
FROM (SELECT node_from AS node_id
FROM roads
WHERE ST_Length(geom) >= 10000.0
UNION
SELECT node_to AS node_id
FROM roads
WHERE ST_Length(geom) >= 10000.0);
----------------------------------------
12630,12648,13645,13651,78353,79142,79453,79454,286140,286153,286763,286770,291416,291417
The SQL aggregate function MakeStringList() is specifically intended to help and simplify this task by applying a pure SQL approach.
SELECT MakeStringList(node_id, ';')
FROM (SELECT node_from AS node_id
FROM roads
WHERE ST_Length(geom) >= 10000.0
UNION
SELECT node_to AS node_id
FROM roads
WHERE ST_Length(geom) >= 10000.0);
----------------------------------------
12630;12648;13645;13651;78353;79142;79453;79454;286140;286153;286763;286770;291416;291417
SELECT MakeStringList(node_id, '|')
FROM (SELECT node_from AS node_id
FROM roads
WHERE ST_Length(geom) >= 10000.0
UNION
SELECT node_to AS node_id
FROM roads
WHERE ST_Length(geom) >= 10000.0);
----------------------------------------
12630|12648|13645|13651|78353|79142|79453|79454|286140|286153|286763|286770|291416|291417
You can eventually pass an optional second argument to MakeStringList() in order to define an alternative separator different from comma.
6 - Solving Isochrone problems
Isochrones are areas (or curves) connecting points at which something occurs or arrives at the same time.Isochrones are usually related to Network Analysis and Routing because they allow to easily identify which specific portion of the Network can be reached starting by some origin Node spending no more than a given Cost.
As you have already seen with multi-destination queries, the Dijkstra's Algorithm robustly ensures that when a destination is reached, all the destinations presenting a lesser cost have also been collected.
This allows to efficiently support Isochrone queries. You simply have to specify a single origin Node and a Cost threshold.
Note: executing an Isochrone query requires a processing time that isn't the sum of all individual timings for each destination, but simply is the time required to reach the most costly destination.
SELECT Algorithm, Request, Role, NodeFrom, NodeTo, Cost, Geometry FROM byfoot WHERE NodeFrom = 181999 AND Cost <= 1000.0;You can call an Isochrone query as supported by VirtualRouting by specifying:
- NodeFrom: the ID or Code uniquely identifying the origin Node.
- Cost: the maximum Cost threshold not to be exceeded.
Note: any valid Isochrone query must necessarily specify a <= (lesser than or equal to) comparison operator.
The following table shows the resultset returned by the above Isochrone query.
| Algorithm | Request | Role | NodeFrom | NodeTo | Cost | Geometry |
|---|---|---|---|---|---|---|
| Dijkstra | Isochrone | Solution | 181999 | 178717 | 572.455143 | BLOB sz=60 GEOMETRY |
| NULL | NULL | Solution | 181999 | 178718 | 587.303779 | BLOB sz=60 GEOMETRY |
| ............. | ||||||
| NULL | NULL | Solution | 181999 | 184035 | 579.786724 | BLOB sz=60 GEOMETRY |
| NULL | NULL | Solution | 181999 | 184036 | 642.691597 | BLOB sz=60 GEOMETRY |
Let's quickly examine the resultset returned by the above isochrone query.
- the first row of the resultset is someway exceptional, and is the only row of the resultset presenting NOT NULL values in the Algorithm, Request, Options (and Delimiter) columns.
- all rows (including the first one) have Role = Solution, and represents a single connection between NodeFrom and NodeTo, with the corresponding Cost.
- the Geometry column always corresponds to the 2D Point where NodeTo is located.
Note: isochrone queries are not affected by configurable options. Algorithm will be always assumed to be Dijsktra, and the current Options settings will be simply ignored.
SELECT ST_ConcaveHull(ST_Collect(Geometry)) FROM byfoot WHERE NodeFrom = 181999 AND Cost <= 1000.0;Any isochrone query will just return a Point-set; if you also wish to obtain the corresponding areal representation you just have to call ST_Collect() in order to get a monolithic MultiPoint, then calling ST_ConcaveHull() in order to get a Polygon.
The map below graphically shows the results of the previous isochrone query.
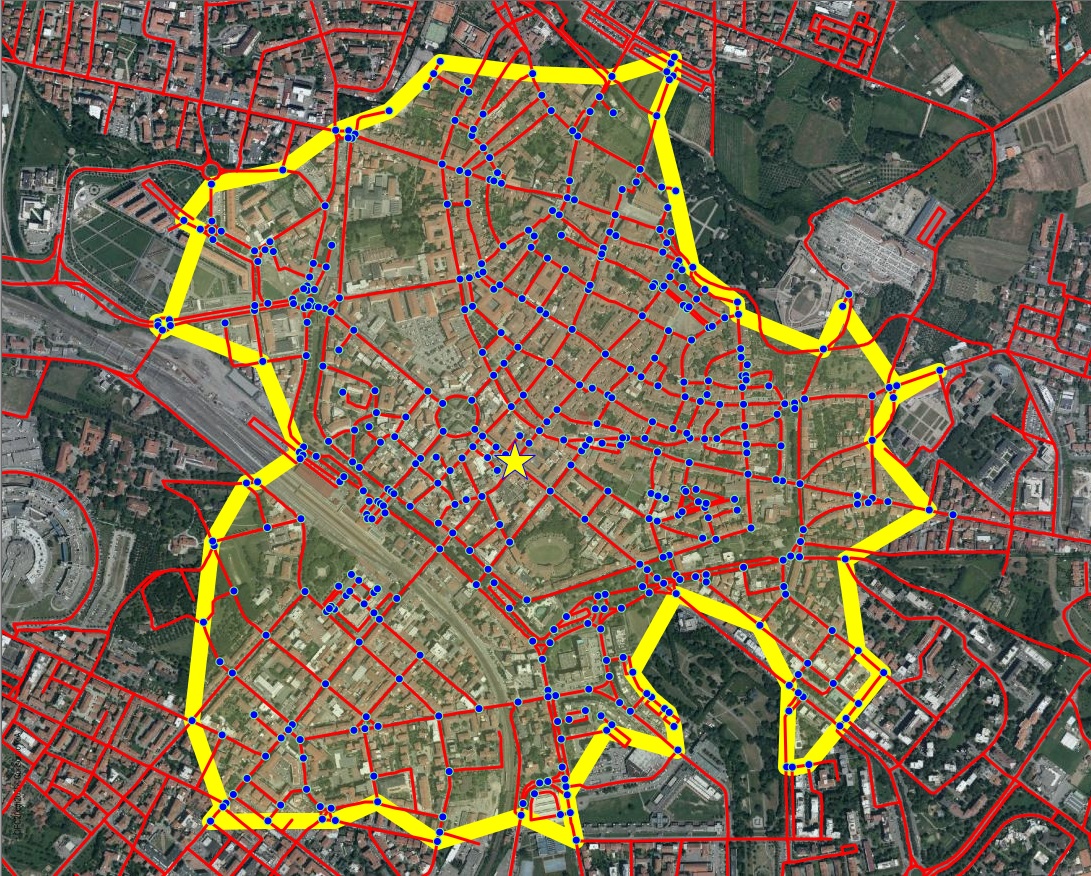
- Yellow star: the Origin Node.
- Blue dots: all Destination Nodes within the given Cost.
- White line: the boundary of the Isochrone.
Note: in this example you've used the byfoot Network, that is based on Costs expressed in meters (geometric length of each Link).
This Network is mainly intended for pedestrians, so we can safely assume a constant speed of about 4 to 6 km/h, and consequently the Isochrone effectively respects the same time requisite.
Speaking in more general terms, an Isochrone can be intended as a generic synonym for same Cost, even when there is no obvious connection with Time..
7 - Solving TSP (traveling salesman) problems
TSP (Traveling Salesman Problem) is a well known Operations Research problem.
The Traveling Salesman Problem
Given a list of cities and the distances between each pair of cities, what is the shortest possible route that visits each city and returns to the origin city ?
Note: the terms salesman and city are universally used for historical reasons, so you should avoid taking them literally and take them in context.
The term salesman in this specific context intends any possible kind of moving agent (pedestrian, vehicle, passenger or whatever else), exactly as city simply stands for any generic destination on a given Network.
We can conceptualy split TPS in two halves:- computing all distances between pairs of cities. This is a typical ShortestPath problem, and we can duly use the Dijkstra's algorithm for this.
- then we have to check for all possible permutations / combinations to identify the optimal TSP solution.
Simply computing the complete TSP solution for about ten cities will require a very long time even using a supercomputer.
And attempting to compute a TSP solution for about hundred cities will require a practically infinite time.
Nevertheless, solving TSP is highly desirable for many application fields: logistics (just think about courier companies as DHL, FedEX, UPS or TNT), field maintenance / assistance, waste collection, schoolbus / shared taxi services etc.
Many algorithms have been invented during last decades intended to produce practical, although approximate / imperfect, TSP solutions in a reasonably short time. Many of them strongly depend on heuristic and / or randomness.
VirtualRouting supports two different TSP algorithms:- TSP NN (aka Nearest Neighbour)
This first algorithm is straightforward, simple and very fast; it can effectively solve huge TSP solutions (a thousand cities or even more) in a very short time.
Short description:- starting from the base city the salesman goes to the city presenting the lesser connection cost.
- the already visited city is removed from the list, and then the salesman goes to the next city presenting, again, the next lesser connection cost.
- the cycle continues until all cities in the list have been visited.
- finally, the salesman returns to his/her initial base city
In the most unlucky case TSP NN could possibly return the worst possible solution, but the specific implementation adopted by VirtualRouting checks against this possibility:- each TSP NN is always computed twice by randomly choosing a different base city and then normalizing the solution; the best of the two solutions is then returned.
- this simple, but effective, precaution ensures that the worst possible solution will never be returned, with a moderately increased execution time.
- TSP GA (aka Genetic Algorithm).
This alternative algorithm is much more complex and sophisticated, and is directly inspired by biological concepts such as sexual reproduction, genetic mutations and natural selection.
Short description:- a first initial set of solutions (the population) is created by using TSP NN after randomly choosing the base city and then normalizing each solution.
- then during each step of the execution loop (generation) pairs of solutions sexually reproduce giving birth to children solutions; reproduction is subject to chromosome crossovers and random mutations.
- for each generation a natural selection (aka elitist selection) process ensures that only the best fit solutions can further propagate their genes to the next generation.
- after a certain number of generations (let's say about some hundredth iterations) the optimal solution (or at least a fairly good sub-optimal solution) should finally emerge, and so the loop can exit.
- Note: TSP GA is usually expected to identify better solutions than TSP NN can do, but it will surely require much more time to complete.
Let's now examine a practical example of TSP solving using VirtualRouting.UPDATE byfoot SET Request = 'TSP'; SELECT Algorithm, Request, Options, Delimiter, RouteId, RouteRow, Role, LinkRowid, NodeFrom, NodeTo, Cost, Geometry, Name FROM byfoot WHERE NodeFrom = 178731 AND NodeTo = '183286,181999,184030,183882,178754';
A VirtualRouting TSP query has the same identical form of a multi-destination query; the base city is always expected to correspond to NodeFrom and all other cities to be visited are expected to be enumerated into a multi-destination list assigned to NodeTo. Note: you must explicitly set the current Request as TSP, TSP NN or TSP GA (TSP and TSP NN are synonyms).
Algorithm Request Options Delimiter RouteId RouteRow Role LinkRowid NodeFrom NodeTo Cost Geometry Name Dijkstra TSP NN Full , [dec=44, hex=2c] 0 0 TSP Solution NULL 178731 178731 1254.433933 BLOB sz=2000 GEOMETRY NULL NULL NULL NULL NULL 1 0 Route NULL 178731 184030 176.364755 BLOB sz=304 GEOMETRY NULL NULL NULL NULL NULL 2 1 Link 224014 178731 182885 94.812424 NULL VIA PIETRO ARETINO NULL NULL NULL NULL 2 2 Link 224862 182885 182043 37.095287 NULL VIA MARGARITONE NULL NULL NULL NULL 2 3 Link 226070 182043 184030 44.457044 NULL PIAZZA SANT'AGOSTINO NULL NULL NULL NULL 2 0 Route NULL 184030 181999 139.114938 BLOB sz=496 GEOMETRY NULL NULL NULL NULL NULL 3 1 Link 226071 184030 182629 55.689009 NULL VIA GIUSEPPE GARIBALDI NULL NULL NULL NULL 3 2 Link 225512 182629 182933 34.184194 NULL CORSO ITALIA NULL NULL NULL NULL 3 3 Link 225511 182933 181999 49.241735 NULL CORSO ITALIA NULL NULL NULL NULL 3 0 Route NULL 181999 183286 217.672885 BLOB sz=688 GEOMETRY NULL NULL NULL NULL NULL 4 1 Link 222635 181999 181998 101.629750 NULL CORSO ITALIA NULL NULL NULL NULL 4 2 Link 224780 181998 183560 73.733572 NULL VIA DELL'ANFITEATRO NULL NULL NULL NULL 4 3 Link 225827 183560 183286 42.309564 NULL VIA DELL'ANFITEATRO NULL NULL NULL NULL 4 0 Route NULL 183286 178754 378.313684 BLOB sz=272 GEOMETRY NULL NULL NULL NULL NULL 5 1 Link 224414 183286 178880 136.372057 NULL VIA MARGARITONE NULL NULL NULL NULL 5 2 Link 219171 178880 178732 93.285538 NULL VIA FRANCESCO CRISPI NULL NULL NULL NULL 5 3 Link 219058 178732 178754 148.656089 NULL VIA FRANCESCO CRISPI NULL NULL NULL NULL 5 0 Route NULL 178754 183882 188.216831 BLOB sz=400 GEOMETRY NULL NULL NULL NULL NULL 6 1 Link 224538 178754 181972 50.900663 NULL VIA ANTONIO GUADAGNOLI NULL NULL NULL NULL 6 2 Link 224537 181972 182000 86.301051 NULL VIA DEL NINFEO NULL NULL NULL NULL 6 3 Link 225527 182000 183882 51.015117 NULL VIA LICIO NENCETTI NULL NULL NULL NULL 6 0 Route NULL 183882 178731 154.750839 BLOB sz=240 GEOMETRY NULL NULL NULL NULL NULL 7 1 Link 225527 183882 182000 51.015117 NULL VIA LICIO NENCETTI NULL NULL NULL NULL 7 2 Link 222636 182000 178731 103.735722 NULL VIA PIETRO ARETINO
Let's now quickly examine the resultset returned by any TSP query:- the general layout is more or less the same as you've already seen in the case of ShortestPath queries.
- the first row of the resultset is someway exceptional, and is the only row of the resultset presenting NOT NULL values in the Algorithm, Request, Options and Delimiter columns.
It contains the TSP solution as a whole: column Cost is the total cost and column Geometry is the overall solution path. - columns RouteId and RouteRow have the same interpretation as in multi-destination ShortestPath queries, but in this specific case each route corresponds to a connection between two cities.
All routes are ordered accordingly to the running sequence of the TSP solution. RouteId=0 identifies the overall TSP solution.
UPDATE byfoot SET Request = 'TSP GA'; SELECT Algorithm, Request, Options, Delimiter, RouteId, RouteRow, Role, LinkRowid, NodeFrom, NodeTo, Cost, Geometry, Name FROM byfoot WHERE NodeFrom = 178731 AND NodeTo = '183286,181999,184030,183882,178754';
If you wish to get a TSP GA solution you simple have to set Request as TSP GA; and you can set again Request as TSP or TSP NN to revert back to the simpler / faster algorithm.
Also in the case of TSP you can eventually activate the Options already explained in the ShortestPath examples.
Note:TSP problems will always imply using the Dijkstra's algorithm, even when the alternative A* algorithm is currently selected.UPDATE byfoot SET Request = 'TSP', Options = 'NO LINKS'; SELECT Algorithm, Request, Options, Delimiter, RouteId, RouteRow, Role, LinkRowid, NodeFrom, NodeTo, Cost, Geometry, Name FROM byfoot WHERE NodeFrom = 178731 AND NodeTo = '183286,181999,184030,183882,178754';
The following table shows a partial resultset that is returned by the same TSP query used in the previous example after enabling the NO LINKS option.
Algorithm Request Options Delimiter RouteId RouteRow Role LinkRowid NodeFrom NodeTo Cost Geometry Name Dijkstra TSP NN No Links , [dec=44, hex=2c] 0 0 TSP Solution NULL 178731 178731 1254.433933 BLOB sz=2000 GEOMETRY NULL NULL NULL NULL NULL 1 0 Route NULL 178731 184030 176.364755 BLOB sz=304 GEOMETRY NULL NULL NULL NULL NULL 2 0 Route NULL 184030 181999 139.114938 BLOB sz=496 GEOMETRY NULL NULL NULL NULL NULL 3 0 Route NULL 181999 183286 217.672885 BLOB sz=688 GEOMETRY NULL NULL NULL NULL NULL 4 0 Route NULL 183286 178754 378.313684 BLOB sz=272 GEOMETRY NULL NULL NULL NULL NULL 5 0 Route NULL 178754 183882 188.216831 BLOB sz=400 GEOMETRY NULL NULL NULL NULL NULL 6 0 Route NULL 183882 178731 154.750839 BLOB sz=240 GEOMETRY NULL
The map below graphically shows the previous TSP queries.
- Red star: the base-city (from where the salesman) begins his/her trip.
- Green dots: the cities to be visited.
- Yellow line: the TSP solution (that is always a circular path).
Warning: how to correctly handling TSP resultsets with spatialite_gui
You should never forget or overlook that both TSP NN and TSP GA are heuristic algorithms heavily relying on random choices.
This could easily have the practical consequence that resolving twice (or even more times) the same identical TSP query could eventually return different resultsets.
There is nothing intrinsically wrong in this, it simply is a direct consequence of using randomness; we are simply bargaining exactness and reproducibility for quickness.
spatialite_gui on its own adopts a paged strategy when showing huge resultsets; this requires repeating the initial SQL query each time that a new page of 500 rows has to be shown on the current window panel.
These two things don't go together well; so don't be surprised when eventually discovering that spatialite_gui will behave bizarrely while presenting some resultset returned by a TSP query.UPDATE byfoot SET Request = 'TSP'; CREATE TABLE my_tsp_solution AS SELECT Algorithm, Request, Options, Delimiter, RouteId, RouteRow, Role, LinkRowid, NodeFrom, NodeTo, Cost, Geometry, Name FROM byfoot WHERE NodeFrom = 178731 AND NodeTo = '183286,181999,184030,183882,178754'; ... <now query "my_tsp_solution" using spatialite_gui> ... DROP TABLE my_tsp_solution;
Hint: resolving this puzzling issue is however basically simple:- you simply have to take a static snapshot of your TSP resultset by using the CREATE TABLE name AS TSP query.
- then you can freely examine the above snapshot.
- and finally you can duly DROP the snapshot once it's no longer useful. (or use CREATE TEMPORARY TABLE name AS TSP query, where the TABLE will be removed at the session end)
More about Linear Referencing and VirtualRouting Linestrings
You have already seen in a previous example that all LINESTRINGs created by VirtualRouting support the M (measure) coordinate intended as a progressive cost for each vertex. And you already know the they can support linear referencing (LR) SQL functions.
Now let's dig in further.Trajectory objects
A Trajectory is any Linestring supporting M coordinates with a continuously increasing trend.
In simpler words, the M-value of each vertex (except the last one) must be lesser than the M-Value of the next vertex.SELECT * FROM my_tsp_solution WHERE ST_IsValidTrajectory(geometry) = 1; ------------------- 1
As you can easily check by calling ST_IsValidTrajectory() every Linestring created by VirtualRouting is a valid Trajectory.SELECT ST_TrajectoryInterpolatePoint(Geometry, 100.0) FROM my_tsp_solution WHERE RouteId = 0;
So you just have to call ST_TrajectoryInterpolatePoint() in order to create a POINT precisely located on the Linestring at the given cost.
The side map graphically shows the estimated positions every 100m assuming the same path returned by the latest TSP query.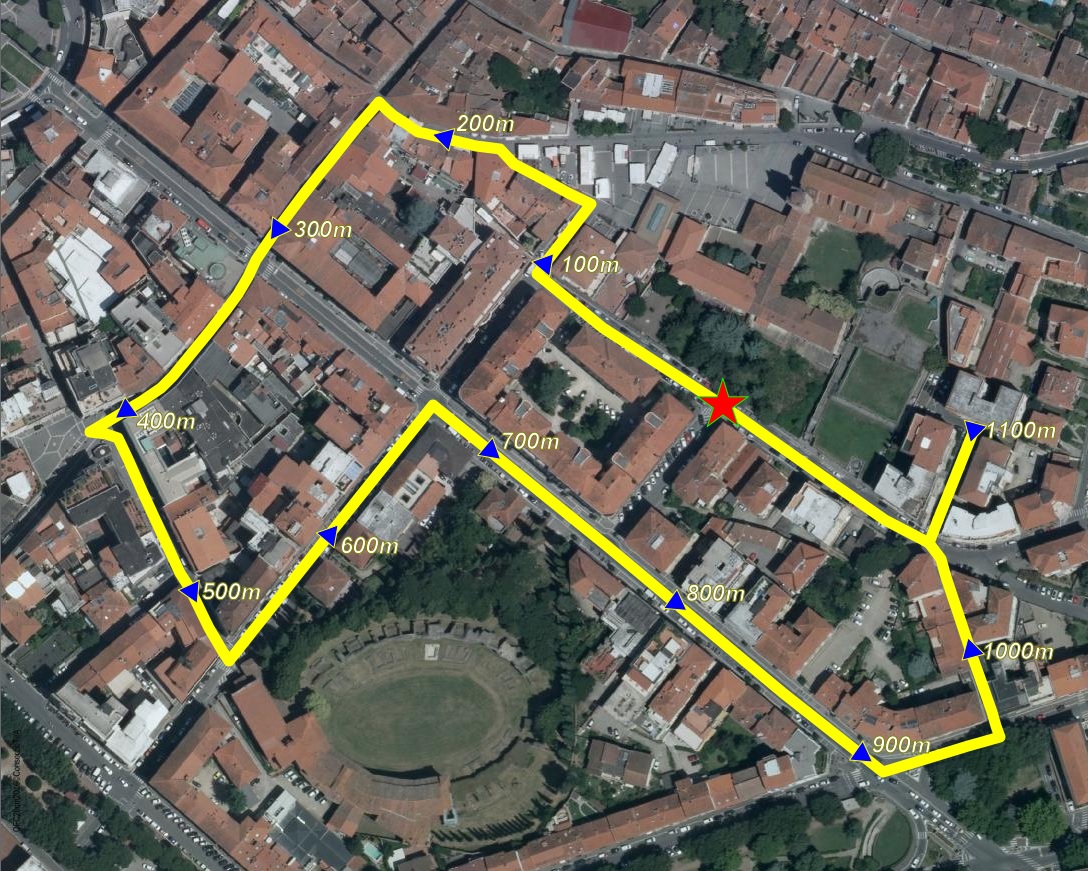
8 - Solving Point-to-Point problems
A Point-to-Point query is very similar to a most usual single-destination Shortest Path query, except that:- A classic Shortest Path query requires to specify a NodeFrom (origin) and a NodeTo (destination).
- A Point-to-Point query has a more relaxed requirement, and just requires to specify a PointFrom (origin) and a PointTo (destination).
Both Points can be freely positioned everywhere on a map, and are not required to precisely intersect either a Node nor a Link of the underlaying Network.
The Point-to-Point's internal logic will then automatically identify (if possible) the appropriate Nodes for computing a Shortest Path solution.
Note: the two Points must use the same SRID of the underlying Network.
How it works in practice
- a first spatial search based on the PointFrom will attempt to identify all Links falling within a given tolerance radius from the Point.
- a second similar spatial search will attempt to identify all Links related to the PointTo.
- all Nodes belonging to any Link identified by the first spatial search will be considered as possible NodeFrom candidates.
- and symmetrically, all Nodes belonging to any Link identified by the second spatial search will be considered as possible NodeTo candidates.
- a full permutation of all Shortest Path solutions connecting one the From candidates to one of the To candidates will be then computed.
- and finally the optimal Point-to-Point solution will be selected by identifying which specific candidate presents the lesser Cost of them all.
Be aware
Attempting to solve Point-to-Point queries strictly requires that an appropriate Spatial Index to effectively support all Links of the underlaying Network.
If such a pre-requirement is not fulfilled the above mentioned spatial searches will fail miserably, and consequently all Point-to-Point queries will be unable to identify any possible Candidate to be evaluated.Always remember
Carefully check if an appropriate Spatial Index allready exists before attempting to execute any Point-to-Point query.
Basic concepts, technical details and related glossary
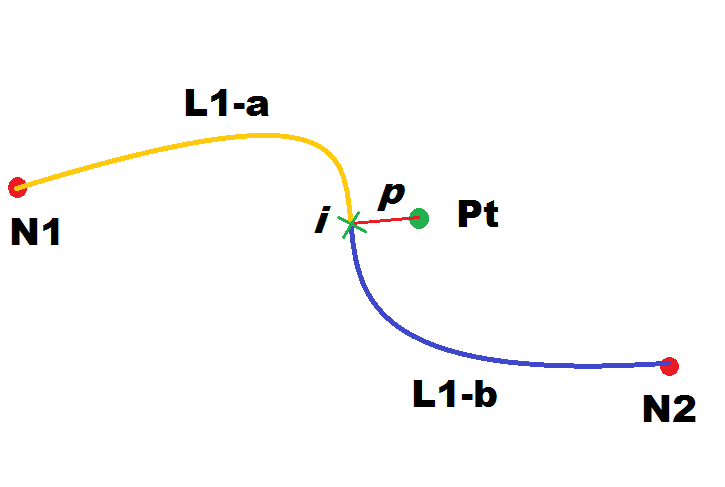
The side figure shows a hypothetical Point-to-Point solution almost precisely based on the following sequence of Nodes:
N1-N2-N3-N4-N5-N6-N7-N8-N9-N10-N11-N12-N13-N14-N15
However, as you can see, there are two noticeable exceptions:- The first Link (connecting N1 to N2) is not completely required by the Solution.
Just a small portion (drawn in red) of this Link is effectively required.
The remaining part (drawn in gray) isn't covered by the Solution. - Exactly the same is true for the last Link connecting N14 to N15.
- That's not all: there are two short segments (drawn in green) connecting Pfrom and Pto (origin and destination Points) respectively to the first and last partial Links.
All this isn't surprising, since it simply is the most obvious direct consequence of the very basic assumptions at the basis of Point-to-Point queries:- Neither the PointFrom nor the PointTo are required to exactly intersect a Node.
Consequently the first and last Links of the overall Point-to-Point Solution could only be partially involved.
In VirtualRouting jargon these two special items are respectively called:- Partial Link (Start)
- Partial Link (End)
- Both the PointFrom and the PointTo can legitimately have been at any arbitrary position and are never required to exactly intersect a Link.
This can easily imply that an extra short leg could be required in order to connect the From/To Points to the corresponding Links.
In VirutalRouting jargon these two special items are respectively called:- Ingress Path
- Egress Path
- Note: none of them are strictly mandatory items:
- the Ingress and/or Egress Paths are not required when the corresponding Point exactly intersects a Link.
- Partial Links (either (Start) or (End)) are never required when the corresponding Point exactly matches a Node.
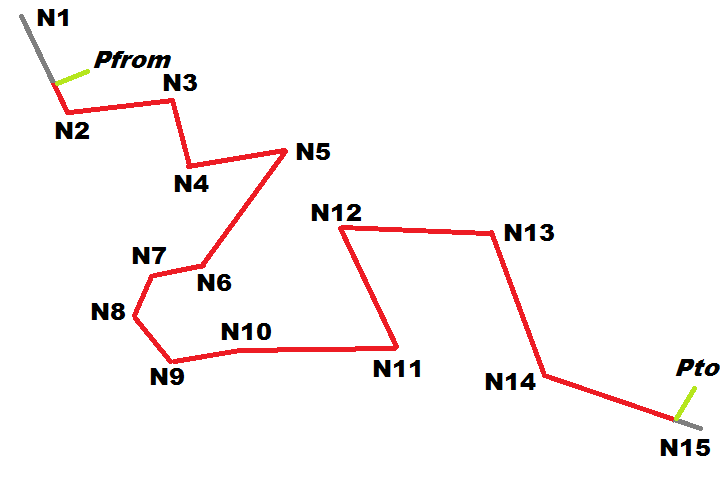
A more comprehensive and detailed explanation based on the side figure: - L1 is a Link connecting Nodes N1 and N2.
- Pt is one between PointFrom or PointTo.
- The Point-to-Point internal logic will start by identifying i, that is the Point intersecting L1 and presenting the minimum distance between the Link and Pt (corresponding to the result returned by calling the ST_Line_Locate_Point() SQL function).
- Now the Link L1 will be split in two halves L1-a and L1-b accordingly to the position of i
(corresponding to the results returned by calling the ST_Line_Substring() SQL function).
Both halves will now be considered as possible Partial Links (Start) candidates leading respectively to N1 or N2; directions will be automatically inverted as required, but only if there are no one-way restrictions.
(the directions will be obviously inverted in the case of Partial Links (End) / NodeTo) - And finally a straight segment p connecting Pt to i will be constructed.
So p exactly corresponds to the Ingress Path if Pt is PointFrom.
(the direction should be obviously inverted in the case of the Egress Path / PointTo)
Warning
VirtualRouting when solving a Point-to-Problem requires a precise estimation of Costs related to Ingress and Egress Paths and to Partial Links.
But VirtualRouting is completely unable to compute complex (and unspecified) Cost formulas, and consequently it will simply assume a Cost corresponding to the Geometric Length of such items.
Conclusion: only Networks based on Costs corresponding to Geometric Lengths can effectively support Point-to-Point queries.
Any different Network configuration will surely lead to wrong and inconsistent results.
Let's now examine a practical example of Point-to-Point solving using VirtualRouting.SELECT Algorithm, Request, Options, RouteId, RouteRow, Role, LinkRowid, NodeFrom, NodeTo, PointFrom, PointTo, Tolerance, Cost, Geometry, Name FROM byfoot WHERE PointFrom = (SELECT geom FROM house_nr_vw WHERE municipality = 'AREZZO' AND address = 'VIA DE'' CENCI 13') AND PointTo = (SELECT geom FROM house_nr_vw WHERE municipality = 'AREZZO' AND address = 'VIA ANTONIO GUADAGNOLI 19/B');A Point-to-Point query has the same form of a single-destination Shortest Path query, except that NodeFrom and NodeTo are now replaced by PointFrom and PointTo.
Note: the sample DB-file supports House Numbers, so you can directly use House Number coordinates as reference Points.
The following table shows the resultset returned by the above Point-to-Point query.
Algorithm Request Options RouteId RouteRow Role LinkRowid NodeFrom NodeTo PointFrom PointTo Tolerance Cost Geometry Name Dijkstra Point2Point Path Full 0 0 Point2Point Solution NULL NULL NULL BLOB sz=68 GEOMETRY BLOB sz=68 GEOMETRY 20.000000 652.815139 BLOB sz=1552 GEOMETRY NULL NULL NULL NULL 0 1 Ingress Path NULL NULL NULL NULL NULL NULL 2.301687 NULL NULL NULL NULL NULL 0 2 Partial Link (Start) 224264 NULL 182630 NULL NULL NULL 46.082761 NULL VIA DE' CENCI NULL NULL NULL 0 3 Link 223758 182630 182629 NULL NULL NULL 24.198115 NULL CORSO ITALIA NULL NULL NULL 0 4 Link 225512 182629 182933 NULL NULL NULL 34.184194 NULL CORSO ITALIA NULL NULL NULL 0 5 Link 225511 182933 181999 NULL NULL NULL 49.241735 NULL CORSO ITALIA NULL NULL NULL 0 6 Link 222635 181999 181998 NULL NULL NULL 101.629750 NULL CORSO ITALIA NULL NULL NULL 0 7 Link 224780 181998 183560 NULL NULL NULL 73.733572 NULL VIA DELL'ANFITEATRO NULL NULL NULL 0 8 Link 225827 183560 183286 NULL NULL NULL 42.309564 NULL VIA DELL'ANFITEATRO NULL NULL NULL 0 9 Link 224897 183286 183128 NULL NULL NULL 72.444609 NULL VIA MARGARITONE NULL NULL NULL 0 10 Link 224232 183128 182890 NULL NULL NULL 103.612221 NULL VIA NICCOLO' ARETINO NULL NULL NULL 0 11 Partial Link (End) 224019 182890 NULL NULL NULL NULL 95.760222 NULL VIA ANTONIO GUADAGNOLI NULL NULL NULL 0 12 Egress Path NULL NULL NULL NULL NULL NULL 7.316709 NULL NULL
Let's now quickly examine the resultset returned by the above Point-to-Point query:- the general layout is almost exactly the same as you've already seen in the case of ShortestPath queries.
- in the specific case of Point-to-Point the first row of the resultset will always contain the followings NOT NULL columns:
- NodeFrom and NodeTo: the two Geometries defining the origin and destination Points.
- Tolerance: the maximum distance allowed between the referenced Points and Candidate Links.
- the Role column can assume one of the following values:
- Point2Point Solution: the header row summarizing the Solution as a whole.
- PointFrom, PointTo and Tolerance columns will have NOT NULL values only in the header row.
- Ingress Path: a straight segment connecting the Origin Point to the first Link.
- Egress Path: a straight segment connecting the last Link to the Destination Point.
- both the Ingress and the Egress Path rows will always have NULL values on LinkRowid, NodeFrom and NodeTo columns.
- Partial Link (Start): the partial section of the first Link.
- this specific row will always have a NULL value on the NodeFrom column.
- Partial Link (End): the partial section of the last Link.
- this specific row will always have a NULL value on the NodeTo column.
- Link: any other Link required by the Point-to-Point Solution.
- all these rows will always have NOT NULL values on LinkRowid, NodeFrom and NodeTo columns.
- Point2Point Solution: the header row summarizing the Solution as a whole.
Point-to-Point queries can be customized, but the configuration rules differ slightly from what you have already seen in the previous examples.- Algorithm: only Dijkstra is supported by Point-to-Point, and will be implicitly assumed even when the alternative A* algorithm is currently selected.
This is because the internal logic of Point-to-Point requires multi-destination queries in order to evaluate all possible Candidate Solutions. - Options: the usual FULL, SIMPLE, NO LINKS and NO GEOMETRIES are supported and will have the same effect as in single-destination queries.
- Tolerance: this setting is specific to Point-to-Point, and defines the maximum allowable distance between a reference Point and Candidate Links.
It defaults to 20.0m if not explicitly set.
UPDATE byfoot SET Options = 'NO GEOMETRIES', Tolerance = 25.5; SELECT Request, Options, Tolerance, RouteRow, Role, LinkRowid, NodeFrom, NodeTo, Cost, Geometry, Name FROM byfoot WHERE PointFrom = (SELECT geom FROM house_nr_vw WHERE municipality = 'AREZZO' AND address = 'VIA DE'' CENCI 13') AND PointTo = (SELECT geom FROM house_nr_vw WHERE municipality = 'AREZZO' AND address = 'VIA ANTONIO GUADAGNOLI 19/C');The following table shows the resultset returned by the above Point-to-Point query after selecting Options = 'NO GEOMETRIES' and Tolerance = 25.5
Request Options Tolerance RouteRow Role LinkRowid NodeFrom NodeTo Cost Geometry Name Point2Point Path No Geometries 25.500000 0 Point2Point Solution NULL NULL NULL 651.067082 NULL NULL NULL NULL NULL 1 Ingress Path NULL NULL NULL 2.301687 NULL NULL NULL NULL NULL 2 Partial Link (Start) 224264 NULL 182630 46.082761 NULL VIA DE' CENCI NULL NULL NULL 3 Link 223758 182630 182629 24.198115 NULL CORSO ITALIA NULL NULL NULL 4 Link 225512 182629 182933 34.184194 NULL CORSO ITALIA NULL NULL NULL 5 Link 225511 182933 181999 49.241735 NULL CORSO ITALIA NULL NULL NULL 6 Link 225800 181999 178880 95.592204 NULL VIA FRANCESCO CRISPI NULL NULL NULL 7 Link 219171 178880 178732 93.285538 NULL VIA FRANCESCO CRISPI NULL NULL NULL 8 Link 219058 178732 178754 148.656089 NULL VIA FRANCESCO CRISPI NULL NULL NULL 9 Partial Link (End) 224019 182890 NULL 150.260641 NULL VIA ANTONIO GUADAGNOLI NULL NULL NULL 10 Egress Path NULL NULL NULL 7.264118 NULL NULL
The map below graphically shows the two Point-to-Point Solutions returned by the previous queries.
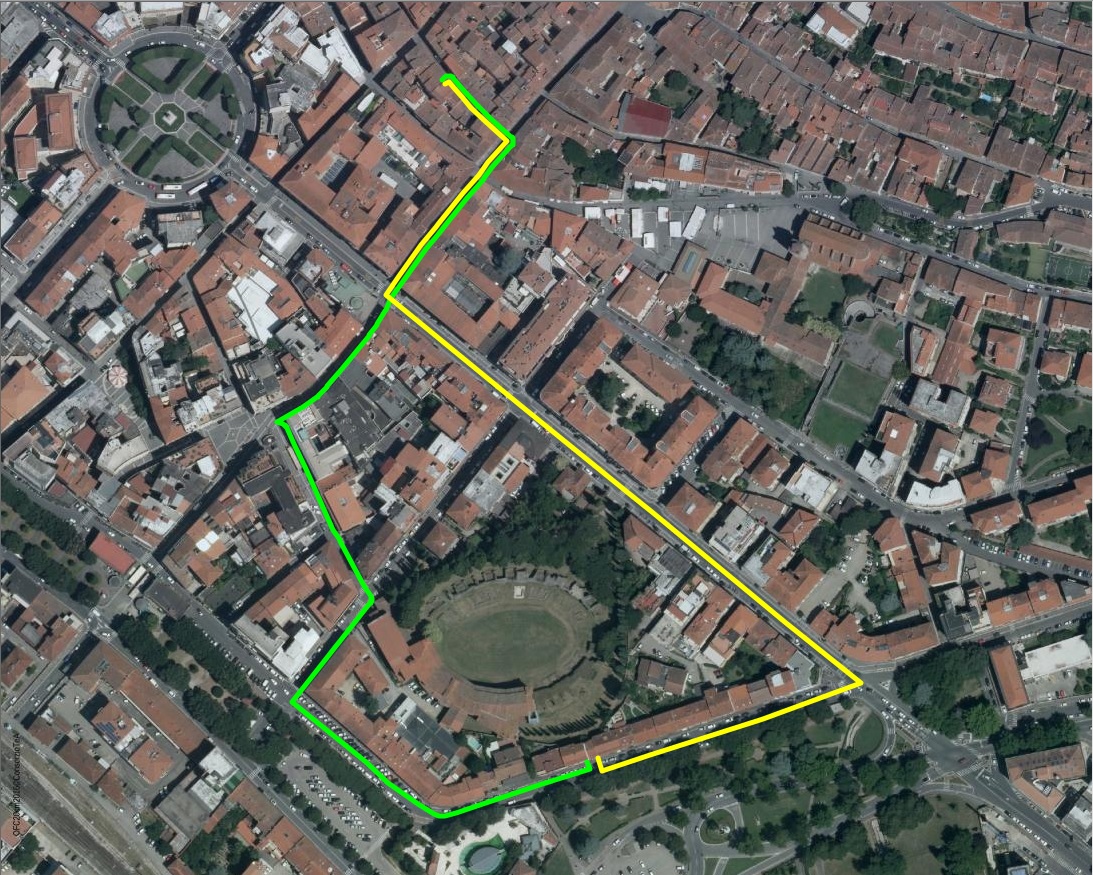
- the green line corresponds to the first solution (PointTo = VIA GUADAGNOLI 19/B).
- the yellow line corresponds to the second solution (PointTo = VIA GUADAGNOLI 19/C).
Note: Point-to-Point queries are very sensitive, and a very bland shift affecting the position of a reference Point could easily cause dramatic changes in the Solution's Path (as is in this case).
Back to 5.0.0-doc main page