Many hyperlinks are disabled.
Use anonymous login
to enable hyperlinks.
Overview
| Artifact ID: |
36b86758363632b1df6a3e5f8247aa0dde32666c
|
|---|
| Page Name: | topo-intro |
|---|
| Date: |
2012-03-12 06:57:09 |
|---|
| Original User: |
bradh
|
|---|
| Parent: |
f9aace1b8b8fa7cafcfc5d2deba29238473c9f02
(diff)
|
|---|
| Next |
484052d1c35a117a14bb43d15b85d2956f075216 |
|---|
Content
|
|
OGC-SFS Geometries
As you already know, the standard representation of Geometries supported by any existing Spatial DBMS is based on the following SFS classes (non-topological):
- (MULTI)POINT
- (MULTI)LINESTRING
- (MULTI)POLYGON
- GEOMETRYCOLLECTION
Topology
An alternative representation (planar graph) is based on the following elements:
- a NODE simply is a notable point, and can be assumed to
be equivalent to SFS POINT.
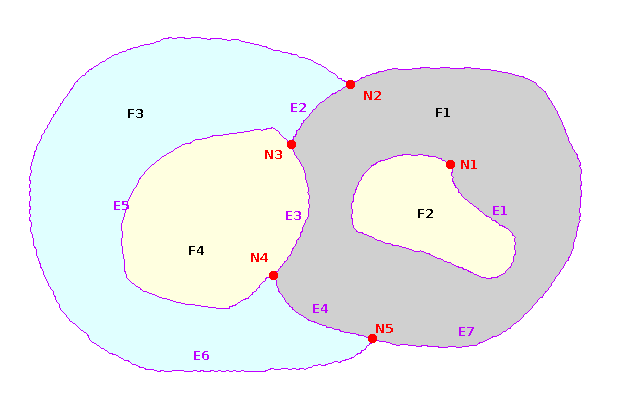
Examples: N1, N2, N3, N4, N5
- an EDGE is an oriented path joining two nodes, and can
be assumed to be equivalent to SFS LINESTRING.
Examples: E1, E2, E3, E4, E5,
E6, E7
- a FACE is a portion of the plane delimited by edges,
and can be assumed to be equivalent to SFS POLYGON.
Examples: F1, F2, F3, F4
- a TopoCurve is a collection of one (or more) Edges, and can
be assumed to be equivalent to SFS MULTILINESTRING.
- a TopoSurface is a collection of one (or more) Faces, and can
be assumed to be equivalent to SFS MULTIPOLYGON.
Example: Faces F2 and F4 belong to the same MultiPolygon.
|
|
|
Constraints on Nodes:
- two (or more) Nodes can never overlap
Constraints on Edges:
- each Edge always has a node-from and a node-to: this implies that any Edge is oriented
- node-from and a node-to may be the same: and in this case we have a self-closed Edge (aka Ring).
Example: E1
- an Edge cannot contain loops (or any other kind of self-intersection)
- two (or more) Edges can intersect only where a Node is defined.
Example: Edges E3, E4 and E5 intersect exactly at Node N4
- no Node can overlap an Edge except at its extremities
Representation of Faces:
- each Face is delimited by a set of Edges: Example: Face F3
is delimited by Edges E2, E5, E4 and E6
- a Face can be delimited by a single Edge: Example: Face F2
is delimited by Edge E1
- a Face must always have an exterior boundary; but can can legitimately have one (or more) interior boundaries
(aka holes) at the same time.
Example: Face F1 is delimited by Edges E1, E2,
E3 and E7
- Edges E2, E3 and E7 represent the exterior boundary
- Edge E1 represents an interior boundary (hole)
|
|