Back to main 4.3.0 Wiki page
Affine Transformations
Starting with version 4.3.0 SpatiaLite supports several new SQL functions based on affine transformations,Understanding and mastering all the underlying mathematics could easily be a rather difficult task, especially if you have absolutely no familiarity with this kind of operation.
So we'll start slowly and simply by first introducing a very simple practical example based on a joke about the geography of Italy and Sicily.
Fancy Geography and amusing Math
Preparing to start
|
|
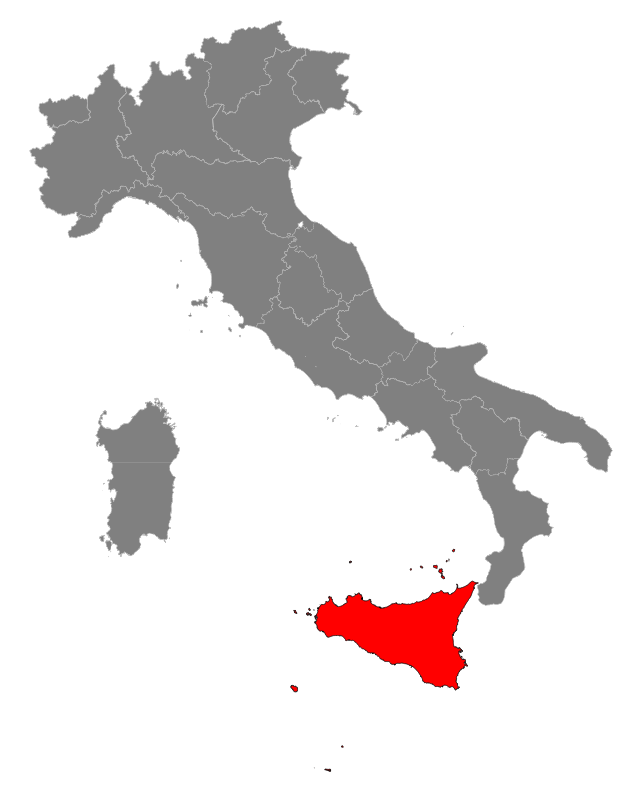
PrefaceLook at a map of Italy; it appears obvious at first glance that Sicily is located in a very inconvenient position:
Incidentally we'll use the new SQL functions based on Affine Transformations for this task. Let's go on. |
|
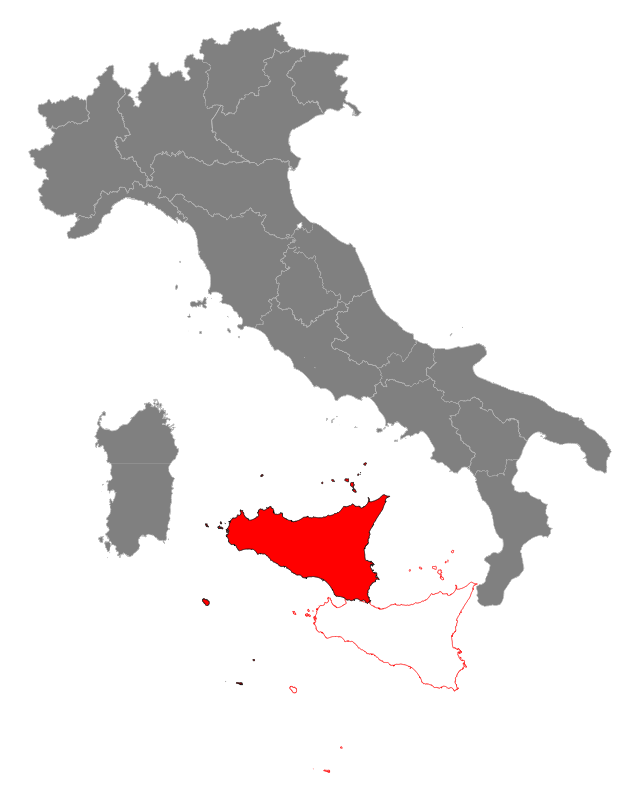
Step #1: translating Sicily into a more convenient positionThere is plenty of free room in the Lower Tyrrhenian Sea, so we'll start by applying a translation to Sicily: this practically means adding (or subtracting) a constant value to the coordinates on both x and y axes.After a very quick examination moving Sicily 150 km (i.e. 150,000 m) westward and 150 km northward seems to be an absolutely reasonable choice. So using the Affine Transformation SQL functions we'll duly execute the following SQL statement:
CREATE TABLE sicilia_1 AS
SELECT cod_reg,
ATM_Transform(geometry,
ATM_CreateTranslate(-150000, 150000)) AS geom
FROM sicilia;
SELECT RecoverGeometryColumn('sicilia_1', 'geom', 32632, 'MULTIPOLYGON', 'XY');
Remarks:
|
|
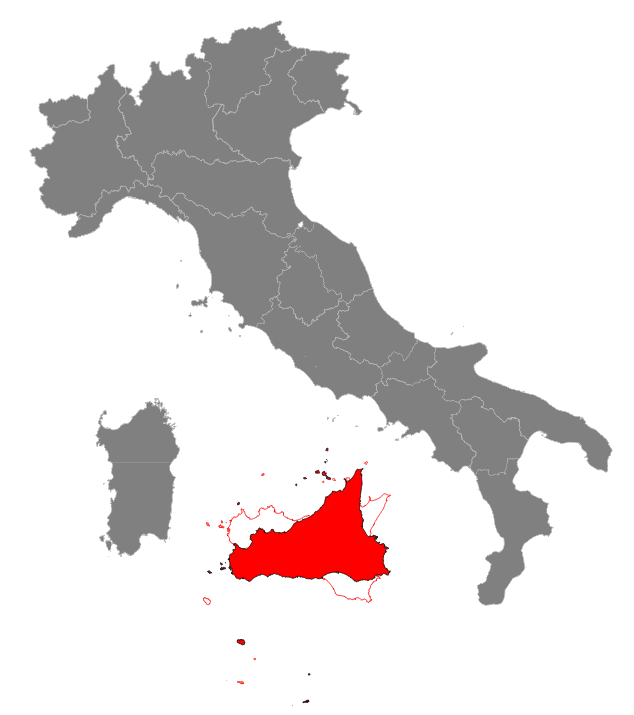
Step #2: rotating Sicily so to get a nice horizontal alignmentAligning the southern shores of Sicily to an almost horizontal line will surely lead to a more nicely ordered layout: so we have now to apply a counterclockwise rotation of about 25.0 degrees.Thanks to Affine Transformations, we can combine both the previous translation and the current rotation into a single movement (a so called rototranslation). We simply have to execute the following SQL statement:
CREATE TABLE sicilia_2 AS
SELECT cod_reg,
ATM_Transform(geometry,
ATM_Translate(
ATM_Translate(
ATM_Rotate(
ATM_CreateTranslate(-cx, -cy),
25),
cx, cy),
-150000, 150000)
) AS geom
FROM (SELECT cod_reg, ST_X(centroid) AS cx, ST_Y(centroid) AS cy, geometry
FROM (SELECT cod_reg, ST_Centroid(geometry) AS centroid, geometry
FROM sicilia) AS g1
) AS g2;
SELECT RecoverGeometryColumn('sicilia_2', 'geom', 32632, 'MULTIPOLYGON', 'XY');
Remarks:
|
|
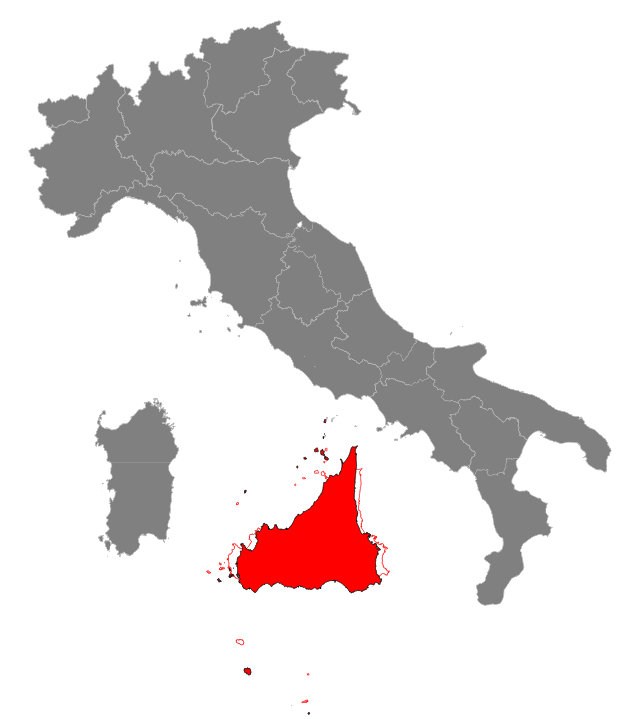
Step #3: inflating and reshaping SicilyAn increased surface is surely welcome, because it automatically implies more agricultural lands: on the other hand shortening a little bit the length of the southern coastline will surely facilitate mobility and communications.So we'll now apply a scaling transformation using two different values: sx=0.9 and sy=1.3. Once again, Affine Transformations enable us to combine altogether both translate, rotate and scale into a single transformation. This is the corresponding SQL statement:
CREATE TABLE sicilia_3 AS
SELECT cod_reg,
ATM_Transform(geometry,
ATM_Translate(
ATM_Translate(
ATM_Scale(
ATM_Rotate(
ATM_CreateTranslate(-cx, -cy),
25),
0.9, 1.3),
cx, cy),
-150000, 150000)
) AS geom
FROM (SELECT cod_reg, ST_X(centroid) AS cx, ST_Y(centroid) AS cy, geometry
FROM (SELECT cod_reg, ST_Centroid(geometry) AS centroid, geometry
FROM sicilia) AS g1
) AS g2;
SELECT RecoverGeometryColumn('sicilia_3', 'geom', 32632, 'MULTIPOLYGON', 'XY');
Remarks:
|
|
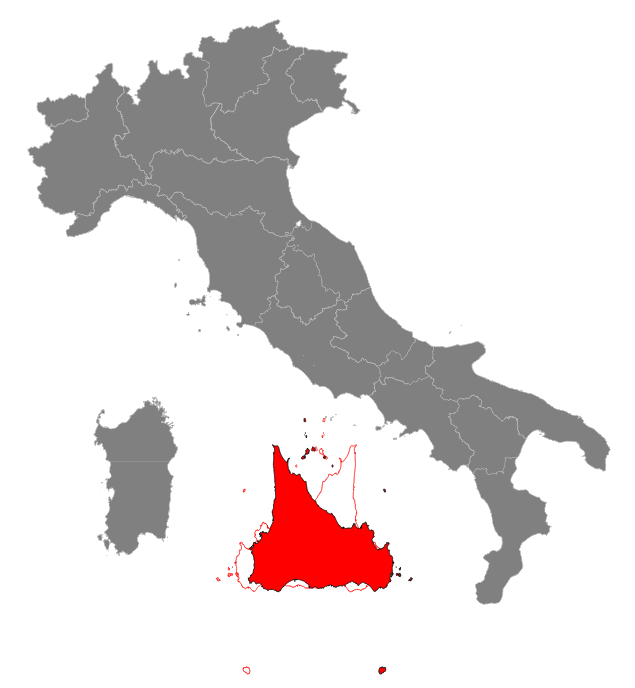
Step #4: final touch: reflecting SicilyA reflected Sicily presents many interesting advantages: we'll examine all them in full detail in the final conclusions of the present study.So we'll now apply a final reflection transformation; this simply corresponds to a 180 degrees rotation around the Y axis. And the following is the final SQL statement applying all the above transformations in a single shot:
CREATE TABLE sicilia_4 AS
SELECT cod_reg,
ATM_Transform(geometry,
ATM_Translate(
ATM_Translate(
ATM_YRoll(
ATM_Scale(
ATM_Rotate(
ATM_CreateTranslate(-cx, -cy),
25),
0.9, 1.3),
180),
cx, cy),
-150000, 150000)
) AS geom
FROM (SELECT cod_reg, ST_X(centroid) AS cx, ST_Y(centroid) AS cy, geometry
FROM (SELECT cod_reg, ST_Centroid(geometry) AS centroid, geometry
FROM sicilia) AS g1
) AS g2;
SELECT RecoverGeometryColumn('sicilia_4', 'geom', 32632, 'MULTIPOLYGON', 'XY');
Remarks:
|
|
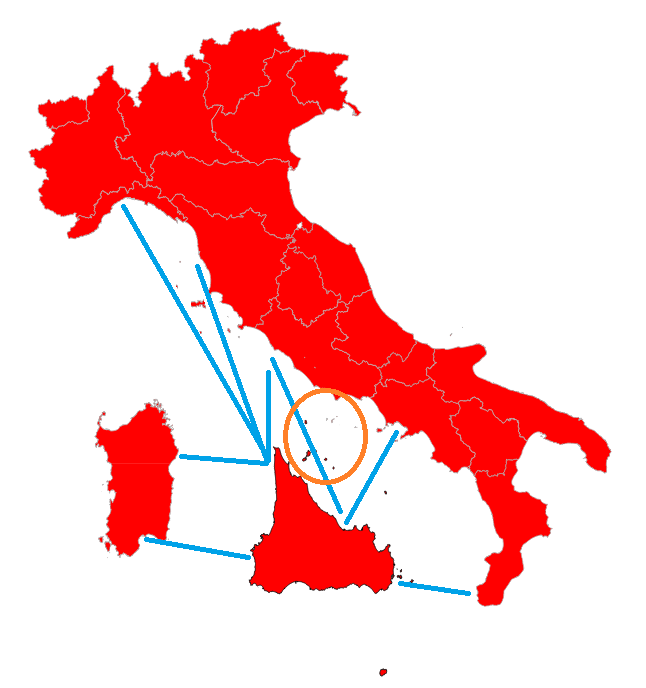
Final considerations and conclusions
|
|
Boring Math: a more formal presentation
Playtime is over: we'll now start a more serious explanation.An Affine Transformation can be represented in the form of a square matrix; the simpler 2D case requires a 3 x 3 matrix, and the followings are the possible arrangements corresponding to each elementary transformation:
| General layout | / | a | b | xoff | \ |
| | | d | e | yoff | | | |
| \ | 0 | 0 | 1 | / | |
| Identity | / | 1 | 0 | 0 | \ |
| | | 0 | 1 | 0 | | | |
| \ | 0 | 0 | 1 | / | |
| Translate(tx, ty) | / | 1 | 0 | tx | \ |
| | | 0 | 1 | ty | | | |
| \ | 0 | 0 | 1 | / | |
| Scale(sx, sy) | / | sx | 0 | 0 | \ |
| | | 0 | sy | 0 | | | |
| \ | 0 | 0 | 1 | / | |
| Rotate(θ) | / | cos(θ) | -sin(θ) | 0 | \ |
| | | sin(θ) | cos(θ) | 0 | | | |
| \ | 0 | 0 | 1 | / | |
A 3D affine transformation requires a 4 x 4 matrix.
As you can easily notice there is an obvious direct relation between a 3D matrix and a 2D matrix; notice the cells showing a gray background.
| General layout | / | a | b | c | xoff | \ |
| | | d | e | f | yoff | | | |
| | | g | h | i | zoff | | | |
| \ | 0 | 0 | 0 | 1 | / | |
| Identity | / | 1 | 0 | 0 | 0 | \ |
| | | 0 | 1 | 0 | 0 | | | |
| \ | 0 | 0 | 1 | 0 | / | |
| \ | 0 | 0 | 0 | 1 | / | |
| Translate(tx, ty, tz) | / | 1 | 0 | 0 | tx | \ |
| | | 0 | 1 | 0 | ty | | | |
| | | 0 | 0 | 1 | tz | | | |
| \ | 0 | 0 | 0 | 1 | / | |
| Scale(sx, sy, sz) | / | sx | 0 | 0 | 0 | \ |
| | | 0 | sy | 0 | 0 | | | |
| | | 0 | 0 | sz | 0 | | | |
| \ | 0 | 0 | 0 | 1 | / | |
| X Roll(θ) | / | 1 | 0 | 0 | 0 | \ |
| | | 0 | cos(θ) | -sin(θ) | 0 | | | |
| | | 0 | sin(θ) | cos(θ) | 0 | | | |
| \ | 0 | 0 | 0 | 1 | / | |
| Y Roll(θ) | / | cos(θ) | 0 | sin(θ) | 0 | \ |
| | | 0 | 1 | 0 | 0 | | | |
| | | -sin(θ) | 0 | cos(θ) | 0 | | | |
| \ | 0 | 0 | 0 | 1 | / | |
| Z Roll(θ) | / | cos(θ) | -sin(θ) | 0 | 0 | \ |
| | | sin(θ) | cos(θ) | 0 | 0 | | | |
| | | 0 | 0 | 1 | 0 | | | |
| \ | 0 | 0 | 0 | 1 | / | |
applying an Affine Transformation
In order to materialize an affine transformation we simply have to compute (x', y', z') coordinates starting from (x, y, z) for every point or vertex found in the input Geometry accordingly to the following formulae:- x' = a*x + b*y + c*z + xoff
- y' = d*x + e*y + f*z + yoff
- z' = g*x + h*y + i*z + zoff
in the simpler 2D case this will assume the reduced form:
- x' = a*x + b*y + xoff
- y' = d*x + e*y + yoff
As you can see, applying an Affine Transformation does not requires computing any trigonometric function.
Trigonometric functions are very costly in computational terms, so applying an Affine Transformation is an intrinsically efficient mechanism because it only requires multiplications and additions.
chaining two (or even more) Affine Transformations in a single operation
Affine transformation matrices have another astonishing property.We can multiply two different affine transformation matrices thus obtaining a third matrix, and this latest once applied will contain both transformations and in the right sequence.
There is no limit; we can infinitely chain as many transformations as required, we'll simply have to continue multiplying all matrices one after the other carefully respecting the appropriate sequence.
At the end of the process we'll always get just a single affine transformation matrix faithfully representing any individual transformation in the chain.
| The multiplication between two matrices is not a commutative operation: the relative order of operands is absolutely relevant. |
multiplying two matrices
Multiplication is not really a simple operation when matrices are involved and requires a rather complex procedure; the following example shows how to multiply two 4 x 4 matrices.
| * |
|
= |
|
identity matrix
An identity matrix simply corresponds to an affine transformation lacking any actual effect: at the end of the process the transformed geometry will be exactly the same as before.Moreover an identity matrix plays a special role in multiplication: the resulting matrix will always be exactly the same of the other matrix.
(it's more or less the equivalent of multiplying e.g. 8*1=8 in an ordinary scalar multiplication).
inverse matrix
If two (non-identity) matrices are such that their multiplication produces an identity matrix they are said to be one the inverse of the other.In simpler words both them cause the same identical trasformations but in exactly opposite ways, so that the final combination simply is a no-op.
Please note: not all Affine Trasformation matrices necessarily have a corresponding inverse matrix.
Boring SQL functions: a formal explanation
| SQL Function | Description |
|---|---|
| ATM_Transform ( BLOB Geometry , BLOB AT-matrix ) : BLOB Geometry | Will return a new Geometry by applying an Affine Transformation to the input Geometry. The output Geometry will preserve the original SRID, dimensions and type. NULL will be returned on invalid arguments. |
| ATM_Transform ( BLOB Geometry , BLOB AT-matrix , int srid ) : BLOB Geometry | Same as above, but the output Geometry will assume the explicitly set SRID. |
| ATM_IsValid ( BLOB AT-matrix ) : BOOLEAN | Will check if a BLOB do really correspond to an encoded Affine Transformation Matrix then returning TRUE or FALSE. -1 will be returned if the argument isn't of the BLOB type. |
| ATM_AsText ( BLOB AT-matrix ) : TEXT | Will return a text serialized representation of the Matrix. NULL will be returned on invalid arguments. |
| basic SQL functions on Affine Transformation Matrix | |
| ATM_Multiply ( BLOB AT-matrix-A , BLOB AT-matrix-B ) : BLOB AT-matrix | Will multiply Matrix-B by Matrix-A then returning the resulting Matrix. NULL will be returned on invalid arguments. |
| ATM_Determinant ( BLOB AT-matrix ) : double | Will return the determinant of the Matrix. NULL will be returned on invalid argument. |
| ATM_IsInvertible ( BLOB AT-matrix ) : boolean | Will return 1 TRUE if the Affine Transformation matrix can be inverted, 0 FALSE if not (only matrices presenting a determinant different from zero can be inverted). NULL will be returned on invalid argument. |
| ATM_Invert ( BLOB AT-matrix ) : BLOB AT-matrix | Will return the inverse matrix. NULL will be returned on invalid argument. |
| SQL functions creating and initializing a new Affine Transformation Matrix | |
| ATM_Create ( void ) : BLOB AT-matrix | Will return an Identity Affine Transformation Matrix. NULL if any error occurs. |
| ATM_Create ( double a , double b , double d , double e , double xoff , double yoff ) : BLOB AT-matrix | Will return a 2D Affine Transformation Matrix initialized with explicit values. NULL if any error occurs or on invalid arguments. |
| ATM_Create ( double a , double b , double c , double d , double e , double f , double g , double h , double i , double xoff , double yoff , double double zoff ) : BLOB AT-matrix | Will return a 3D Affine Transformation Matrix initialized with explicit values. NULL if any error occurs or on invalid arguments. |
| ATM_CreateTranslate ( double tx , double ty ) : BLOB AT-matrix ATM_CreateTranslate ( double tx , double ty , double tz ) : BLOB AT-matrix | Will return an Affine Transformation Matrix initialized respectively as a 2D or 3D Translate. NULL if any error occurs or on invalid arguments. |
| ATM_CreateScale ( double sx , double sy ) : BLOB AT-matrix ATM_CreateScale ( double sx , double sy , double sz ) : BLOB AT-matrix | Will return an Affine Transformation Matrix initialized respectively as a 2D or 3D Scale. NULL if any error occurs or on invalid arguments.. |
| ATM_CreateRotate ( double angleInDegrees ) : BLOB AT-matrix ATM_CreateZRoll ( double angleInDegrees ) : BLOB AT-matrix | Will return an Affine Transformation Matrix initialized as Rotation around the Z axis. NULL if any error occurs or on invalid arguments. The angle is always expected to be measured in decimal degrees. The direction of rotation is defined such that positive angles rotate in the direction from the positive X axis toward the positive Y axis. With the default axis orientation positive angles rotate in a counterclockwise direction. Note: this is the unique rotation allowed on a purely 2D plane. |
| ATM_CreateXRoll ( double angleInDegrees ) : BLOB AT-matrix | Will return an Affine Transformation Matrix initialized as Rotation around the X axis. NULL if any error occurs or on invalid arguments. |
| ATM_CreateYRoll ( double angleInDegrees ) : BLOB AT-matrix | Will return an Affine Transformation Matrix initialized as Rotation around the Y axis. NULL if any error occurs or on invalid arguments. |
| SQL functions supporting chaining two Affine Transformation Matrices | |
| ATM_Translate ( BLOB AT-matrix , double tx , double ty ) : BLOB AT-matrix ATM_Translate ( BLOB AT-matrix , double tx , double ty , double tz ) : BLOB AT-matrix | Will return an Affine Transformation Matrix by chaining respectively a 2D or 3D Translate and another Affine Transformation. NULL if any error occurs or on invalid arguments. |
| ATM_Scale ( BLOB AT-matrix , double sx , double sy ) : BLOB AT-matrix ATM_Scale ( BLOB AT-matrix , double sx , double sy , double sz ) : BLOB AT-matrix | Will return an Affine Transformation Matrix by chaining respectively a 2D or 3D Scale and another Affine Transformation. NULL if any error occurs or on invalid arguments.. |
| ATM_Rotate ( BLOB AT-matrix , double angleInDegrees ) : BLOB AT-matrix ATM_ZRoll ( BLOB AT-matrix , double angleInDegrees ) : BLOB AT-matrix | Will return an Affine Transformation Matrix by chaining a Rotation around the Z axis and another Affine Transformation. NULL if any error occurs or on invalid arguments. |
| ATM_XRoll ( BLOB AT-matrix , double angleInDegrees ) : BLOB AT-matrix | Will return an Affine Transformation Matrix by chaining a Rotation around the X axis and another Affine Transformation. NULL if any error occurs or on invalid arguments. |
| ATM_YRoll ( BLOB AT-matrix , double angleInDegrees ) : BLOB AT-matrix | Will return an Affine Transformation Matrix by chaining a Rotation around the Y axis and another Affine Transformation. NULL if any error occurs or on invalid arguments. |
Note: all the above functions simply are convenience methods intended to avoid any need to repeatedly call ATM_Multiply().
SELECT ATM_Multiply(ATM_CreateRotate(15),
ATM_Multiply(ATM_CreateScale(1.1, 1.2, 1.3),
ATM_CreateTranslate(10, 20, 30)));
SELECT ATM_Rotate(
ATM_Scale(
ATM_CreateTranslate(10, 20, 30),
1.1, 1.2, 1.3),
15);
SELECT ATM_Rotate(
ATM_Scale(
ATM_Translate(
ATM_Create(),
10, 20, 30),
1.1, 1.2, 1.3),
15);
All three statements will return exactly the same identical Affine Transformation Matrix; anyway the second notation is obviously most concise and more practical than the other two.Note: in any complex chain of transformations the innermost operation will be applied first, and the outermost operation will be applied last. | |