what's this SRID stuff ? ...
I've never heard this term before now ...
Note: these pages are no longer maintainedNever the less, much of the information is still relevant.Beware, however, that some of the command syntax is from older versions, and thus may no longer work as expected. Also: external links, from external sources, inside these pages may no longer function. |
|
what's this SRID stuff ? ... |
| 2011 January 28 |
| Previous Slide | Table of Contents | Next Slide |
|
What's this SRID stuff ? ... I've never heard this term before now ... Planet Earth is a sphere ... not exactly, planet Earth has an ellipsoidal shape (slightly flattened at poles) ...oh no, that's absolutely wrong: planet Earth hasn't a geometric regular shape, it actually is a geoid All the above assertions can be assumed to be true, but at different approximation levels. Near the Equator differences between a sphere and an ellipsoid are rather slight and quite unnoticeable; but neat both Poles such differences becomes greater and most easily appreciable. For many practical purposes differences between an ellipsoid and a geoid are very slim: but for long range aircraft navigation (or even worse, for satellite positioning), this is too much simplistic and unacceptably approximate. 
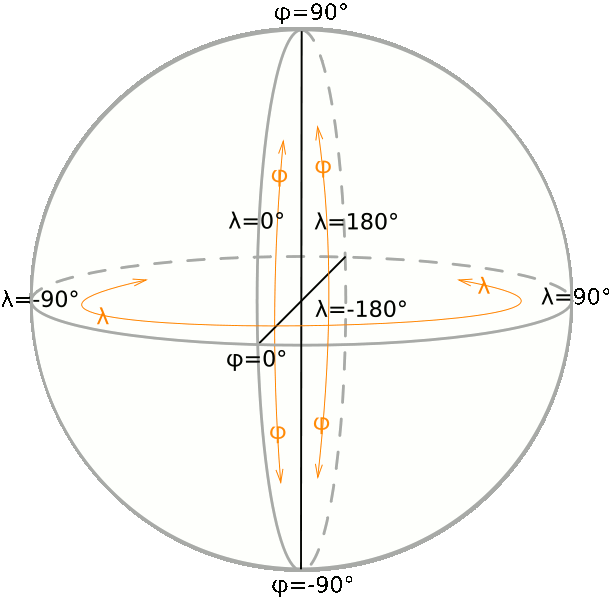
Anyway, whatsoever could be the real shape of the Earth, position of each point on the planet surface can precisely determined simply measuring two angles: longitude and latitude. In order to set a complete Spatial Reference System [aka SRS] we can use the Poles and the Equator (which after all are outstanding places by intrinsic astronomic properties): choosing a Prime Meridian on the other side is absolutely conventional: but since many centuries (Britannia rule the waves ...) adopting the Greenwich Meridian is an obvious choice. Any SRS based on long-lat coordinates is known as a Geographic System. Using a Geographic SRS surely grants you maximum precision and accuracy: but unhappily this fatally implies several undesirable side-effects:
All them introduce some degree of approximation and deformation: choosing the one or the other implies an absolutely arbitrary and conventional process: a map projection good to represent small Earth's portions can easily be awful when used to represent very wide territories, and vice versa. We'll quickly examine the UTM [Universal Transverse Mercator] map projection, simply because it's really often used. 
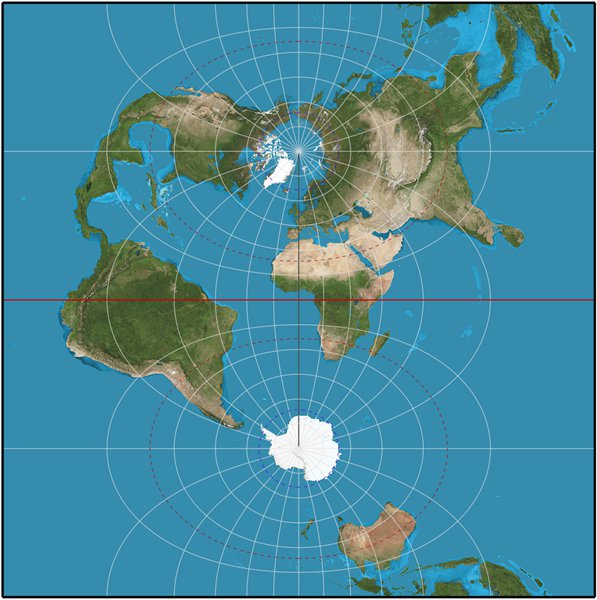
Apparently this map projection introduces severe and not acceptable deformations: but when you carefully focus your attention on the narrow central fuse, you'll immediately recognize that UTM allows to get a nearly perfect planar projection of excellent quality. Anyway all this has a price: the central fuse has to be really narrow (let say, it will span only few degrees on both sides). As the fuse becomes wider, as much more deformations will become stronger and more evident. 
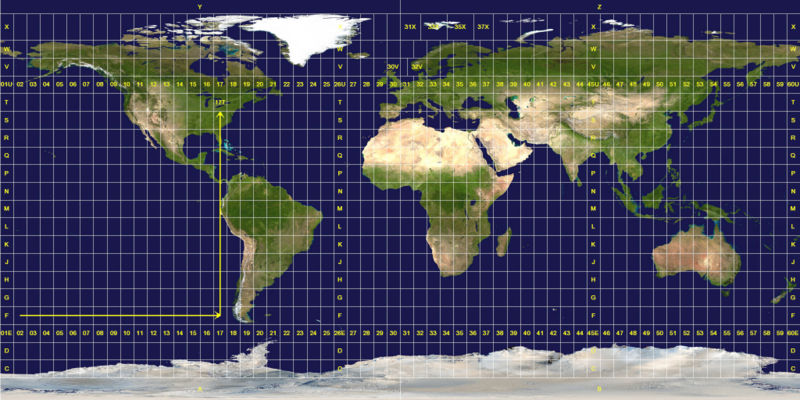
Accordingly to all the above considerations, UTM defines 60 standard zones, each one covering exactly 6 longitude degrees. Merging together two adjacent fuses (12 degrees) obviously reduces accuracy, but is still acceptable for many practical purposes: exceeding this limit produces really low-quality results, and has to be absolutely avoided. Attempting to standardize the chaos During the past two centuries every National State has introduced at least one (and very often, more than one) map projection system and related SRS: the overall result is absolutely chaotic (and really painful to be handled). Happily, an international standard is widely adopted so to make easier correctly handling map SRS: the European Petroleum Survey Group [EPSG] maintains a huge worldwide dataset of more than 3,700 different entries. Many of them are nowadays obsolete, and simply play a historical role; many others are only useful in very limited national boundaries. Anyway, this one is an absolutely impressive collection. And each single entry within the EPSG dataset is uniquely identified by its numeric ID and descriptive name, so to avoid any possible confusion and ambiguity. Any Spatial DBMS requires some SRID-value to be specified for each Geometry: but such SRID simply is a Spatial Reference ID, and (hopefully) coincides with the corresponding EPSG ID Just in order to help you understand better this SRID chaos, this is a quite complete list of SRIDs often used in a (small) Nation such as Italy:
And the following examples may help to understand even better:
As you can easily notice:
And now we can examine how using different SRSes affects distances:
But this isn't at all surprising in physical and natural sciences: any measured value is intrinsically affected by errors and approximations. And any calculated value will be inexorably affected by rounding and truncation artifacts. So absolutely exact figures simply doesn't exist in the real world: you have to be conscious that you can simply get some more or less approximated value. But at least, you can take care to properly reduce such approximations in the best possible way. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Previous Slide | Table of Contents | Next Slide |
| Author: Alessandro Furieri a.furieri@lqt.it |
| This work is licensed under the Attribution-ShareAlike 3.0 Unported (CC BY-SA 3.0) license. | |
 |
Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version 1.3 or any later version published by the Free Software Foundation; with no Invariant Sections, no Front-Cover Texts, and no Back-Cover Texts. |